4.1 Random Forest Classifiers

Random Forests are supervised machine learning methods that belong to the class of ensemble methods [215–217]. They are easy to implement, fast to train and can handle large numbers of features due to implicit feature selection [218].

Ensemble methods combine the predictions of several independent base estimators with the goal to improve generalizability over a single estimator. Random forests are ensembles of decision trees where randomness is introduced in two ways:

  1. every tree is build on a random sample that is drawn with replacement from the training set and has the same size as the training set (i.e., a bootstrap sample)
  2. every split of a node is evaluated on a random subset of features

A single decision tree, especially when it is grown very deep is highly susceptible to noise in the training set and therefore prone to overfitting which results in poor generalization ability. As a consequence of randomness and averaging over many decision trees, the variance of a random forest predictor decreases and therefore the risk of overfitting [219]. It is still advisable to restrict the depth of single trees in a random forest, not only to counteract overfitting but also to reduce model complexity and to speedup the algorithm.

Random forests are capable of regression and classification tasks. For classification, predictions for new data are obtained by running each data sample down every tree in the forest and then either apply majority voting over single class votes or averaging the probabilistic class predictions. Probabilistic class predictions of single trees are computed as the fraction of training set samples of the same class in a leaf whereas the single class vote refers to the majority class in a leaf. Figure 4.1 visualizes the procedure of classifying a new data sample.

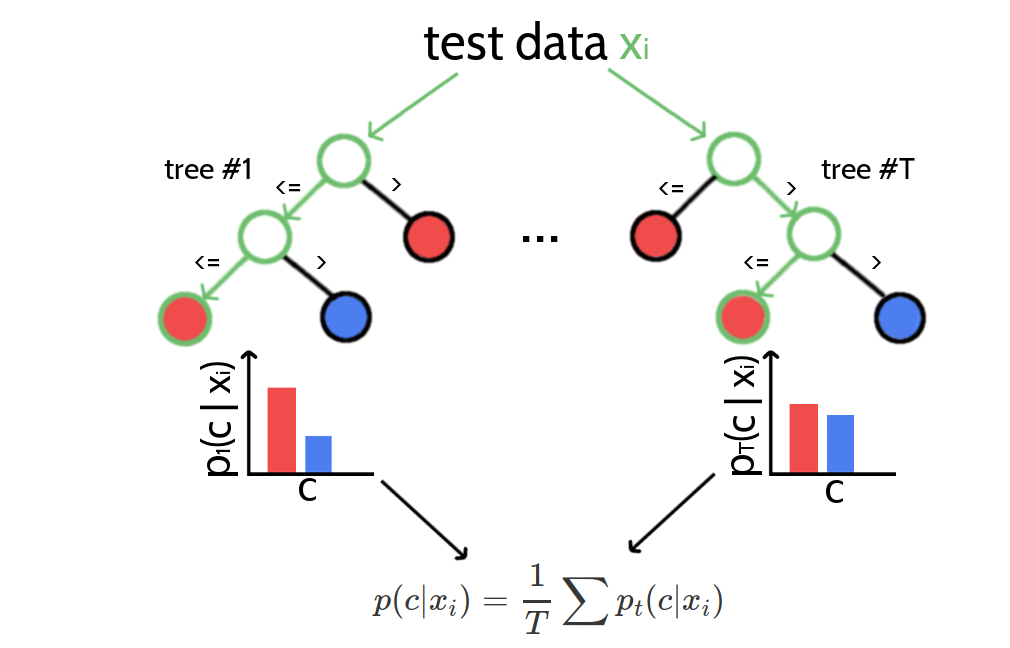
Classifying new data with random forests. A new data sample is run down every tree in the forest until it ends up in a leaf node. Every leaf node has associated class probabilities \(p(c)\) reflecting the fraction of training samples at this leaf node belonging to every class \(c\). The color of the leaf nodes reflects the class with highest probability. The predictions from all trees in form of the class probabilties are averaged and yield the final prediction.

Figure 4.1: Classifying new data with random forests. A new data sample is run down every tree in the forest until it ends up in a leaf node. Every leaf node has associated class probabilities \(p(c)\) reflecting the fraction of training samples at this leaf node belonging to every class \(c\). The color of the leaf nodes reflects the class with highest probability. The predictions from all trees in form of the class probabilties are averaged and yield the final prediction.

Typically, Gini impurity, which is a computationally efficient approximation to the entropy, is used as a split criterion to evaluate the quality of a split. It measures the degree of purity in a data set regarding class labels as \(GI = (1 - \sum_{k=1}^K p_k^2)\), where \(p_k\) is the proportion of class \(k\) in the data set. For every feature \(f\) in the random subset that is considered for splitting a particular node \(N\), the decrease in Gini impurity \(\Delta GI_f\) will be computed as,

\[ \Delta GI_f(N_{\textrm{parent}}) = GI_f(N_{\textrm{parent}}) - p_{\textrm{left}} GI_f(N_{\textrm{left}}) - p_{\textrm{right}} GI_f(N_{\textrm{left}}) \]

where \(p_{\textrm{left}}\) and \(p_{\textrm{right}}\) refers to the fraction of samples ending up in the left and right child node respectively [218]. The feature \(f\) with highest \(\Delta GI_f\) over the two resulting child node subsets will be used to split the data set at the given node \(N\).

Summing the decrease in Gini impurity for a feature \(f\) over all trees whenever \(f\) was used for a split yields the Gini importance measure, which can be used as an estimate of general feature relevance. Random forests therefore are popular methods for feature selection and it is common practice to remove the least important features from a data set to reduce the complexity of the model. However, feature importance measured with respect to Gini importance needs to be interpreted with care. The random forest model cannot distinguish between correlated features and it will choose any of the correlated features for a split, thereby reducing the importance of the other features and introducing bias. Furthermore, it has been found that feature selection based on Gini importance is biased towards selecting features with more categories as they will be chosen more often for splits and therefore tend to obtain higher scores [220].

References

215. Ho, T.K. (1998). The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 20, 832–844., doi: 10.1109/34.709601.

217. Breiman, L. (2001). Random Forests. Mach. Learn. 45, 5–32., doi: 10.1023/A:1010933404324.

218. Menze, B.H., Kelm, B.M., Masuch, R., Himmelreich, U., Bachert, P., Petrich, W., and Hamprecht, F.A. (2009). A comparison of random forest and its Gini importance with standard chemometric methods for the feature selection and classification of spectral data. BMC Bioinformatics 10, 213., doi: 10.1186/1471-2105-10-213.

219. Louppe, G. (2014). Understanding Random Forests: From Theory to Practice.

220. Strobl, C., Boulesteix, A.-L., Zeileis, A., and Hothorn, T. (2007). Bias in random forest variable importance measures: Illustrations, sources and a solution. BMC Bioinformatics 8, 25., doi: 10.1186/1471-2105-8-25.