PhD thesis: residue-residue contact prediction

3.7 Methods

3.7.1 The Potts Model

The $N$ sequences of the MSA $\X$ of a protein family are denoted as ${\seq_1, ..., \seq_N}$. Each sequence $\seq_n = (\seq_{n1}, ..., \seq_{nL})$ is a string of $L$ letters from an alphabet indexed by $\{0, ..., 20\}$, where 0 stands for a gap and $\{1, ... , 20\}$ stand for the 20 types of amino acids. The likelihood of the sequences in the MSA of the protein family is modelled with a Potts Model, as described in detail in section 1.2.4:

\[\begin{align} p(\X | \v, \w) &= \prod_{n=1}^N p(\seq_n | \v, \w) \nonumber \\ &= \prod_{n=1}^N \frac{1}{Z(\v, \w)} \exp \left( \sum_{i=1}^L v_i(x_{ni}) \sum_{1 \leq i < j \leq L} w_{ij}(x_{ni}, x_{nj}) \right) \end{align}\]

The coefficients $\via$ and $\wijab$ are referred to as single potentials and couplings, respectively that describe the tendency of an amino acid a (and b) to (co-)occur at the respective positions in the MSA. $Z(\v, \w)$ is the partition function that normalizes the probability distribution $p(\seq_n |\v, \w)$:

\[\begin{equation} Z(\v, \w) = \sum_{y_1, ..., y_L = 1}^{20} \exp \left( \sum_{i=1}^L v_i(y_i) \sum_{1 \leq i < j \leq L} w_{ij}(y_i, y_j) \right) \end{equation}\] The log likelihood is \[\begin{align} \LL &= \log p(\X | \v, \w) \nonumber \\ &= \sum_{n=1}^N \left [ \sum_{i=1}^L v_i(x_{ni}) \sum_{1 \leq i < j \leq L} w_{ij}(x_{ni}, x_{nj}) \right ] - N \log Z(\v, \w) . \end{align}\] The gradient of the log likelihood has single components \[\begin{align} \frac{\partial \LL}{\partial \via} &= \sum_{n=1}^N I(x_{ni} \eq a) - N \frac{\partial}{\partial \via} \log Z(\v,\w) \nonumber\\ &= \sum_{n=1}^N I(x_{ni} \eq a) - N \sum_{y_1,\ldots,y_L=1}^{20} \!\! \frac{ \exp \left( \sum_{i=1}^L v_i(y_i) + \sum_{1 \le i < j \le L} w_{ij}(y_i,y_j) \right)}{Z(\v,\w)} I(y_i \eq a) \nonumber\\ &= N q(x_{i} \eq a) - N p(x_i \eq a | \v,\w) \tag{3.5} \end{align}\]

and pair components

\[\begin{align} \frac{\partial \LL}{\partial \wijab} =& \sum_{n=1}^N I(x_{ni}=a, x_{nj}=b) - N \frac{\partial}{\partial \wijab} \log Z(\v,\w) \nonumber\\ =& \sum_{n=1}^N I(x_{ni} \eq a, x_{nj} \eq b) \nonumber\\ & - N \sum_{y_1,\ldots,y_L=1}^{20} \!\! \frac{ \exp \left( \sum_{i=1}^L v_i(y_i) + \sum_{1 \le i < j \le L} w_{ij}(y_i,y_j) \right)}{Z(\v,\w)} I(y_i \eq a, y_j \eq b) \nonumber\\ =& N q(x_{i} \eq a, x_{j} \eq b) - N \sum_{y_1,\ldots,y_L=1}^{20} p(y_1, \ldots, y_L | \v,\w) \, I(y_i \eq a, y_j \eq b) \nonumber\\ =& N q(x_{i} \eq a, x_{j} \eq b) - N p(x_i \eq a, x_j \eq b | \v,\w) \tag{3.6} \end{align}\]

3.7.2 Treating Gaps as Missing Information

Treating gaps explicitly as 0’th letter of the alphabet will lead to couplings between columns that are not in physical contact. To see why, imagine a hypothetical alignment consisting of two sets of sequences as it is illustrated in Figure 3.27. The first set has sequences covering only the left half of columns in the MSA, while the second set has sequences covering only the right half of columns. The two blocks could correspond to protein domains that were aligned to a single query sequence. Now consider couplings between a pair of columns $i, j$ with $i$ from the left half and $j$ from the right half. Since no sequence (except the single query sequence) overlaps both domains, the empirical amino acid pair frequencies $q(x_i = a, x_j = b)$ will vanish for all $a, b \in \{1,... , L\}$.

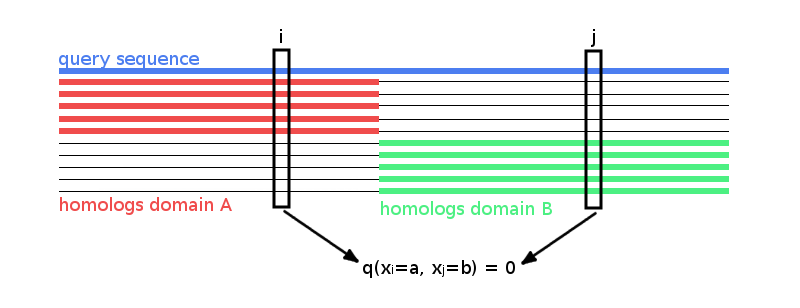
$Hypothetical MSA consisting of two sets of sequences: the first set has sequences covering only the left half of columns, while the second set has sequences covering only the right half of columns. The two blocks could correspond to protein domains that were aligned to a single query sequence. Empirical amino acid pair frequencies $q(x_i \eq a, x_j \eq b)$ will vanish for positions $i$ from the left half and $j$ from the right half of the alignment.$

Figure 3.27: Hypothetical MSA consisting of two sets of sequences: the first set has sequences covering only the left half of columns, while the second set has sequences covering only the right half of columns. The two blocks could correspond to protein domains that were aligned to a single query sequence. Empirical amino acid pair frequencies $q(x_i \eq a, x_j \eq b)$ will vanish for positions $i$ from the left half and $j$ from the right half of the alignment.

According to the gradient of the log likelihood for couplings $\wijab$ given in eq (3.6), the empirical frequencies $q(x_{i} \eq a, x_{j} \eq b)$ are equal to the model probabilities $p(x_i \eq a, x_j \eq b | \v,\w)$ at the maximum of the likelihood when the gradient vanishes. Therefore, $p(x_i \eq a, x_j \eq b | \v, \w)$ would have to be zero at the optimum when the empirical amino acid frequencies $q(x_i \eq a, x_j \eq b)$ vanish for pairs of columns as described above. However, $p(x_i \eq a, x_j \eq b | \v, \w)$ can only become zero, when the exponential term is zero, which would only be possible if $\wijab$ goes to $−\infty$. This is clearly undesirable, as physical contacts will be deduced from the size of the couplings.

The solution is to treat gaps as missing information. This means that the normalisation of $p(\seq_n | \v, \w)$ should not run over all positions $i \in \{1,... , L\}$ but only over those $i$ that are not gaps in $\seq_n$. Therefore, the set of sequences $\Sn$ used for normalization of $p(\seq_n | \v, \w)$ in the partition function will be defined as:

\[\begin{equation} \Sn := \{(y_1,... , y_L): 0 \leq y_i \leq 20 \land (y_i \eq 0 \textrm{ iff } x_{ni} \eq 0) \} \end{equation}\]

and the partition function becomes:

\[\begin{equation} Z_n(\v, \w) = \sum_{\mathbf{y} \in \Sn} \exp \left( \sum_{i=1}^L v_i(y_i) \sum_{1 \leq i < j \leq L} w_{ij}(y_i, y_j) \right) \end{equation}\]

To ensure that the gaps in $y \in \Sn$ do not contribute anything to the sums, the parameters associated with a gap will be fixed to 0 \[ \vi(0) = \wij(0, b) = \wij(a, 0) = 0 \; , \] for all $i, j \in \{1, ..., L\}$ and $a, b \in \{0, ..., 20\}$.

Furthermore, the empirical amino acid frequencies $q_{ia}$ and $q_{ijab}$ need to be redefined such that they are normalised over $\{1, ..., 20\}$,

\[\begin{align} N_i :=& \sum_{n=1}^N w_n I(x_{ni} \!\ne\! 0) & q_{ia} = q(x_i \eq a) :=& \frac{1}{N_i} \sum_{n=1}^N w_n I(x_{ni} \eq a) \\ N_{ij} :=& \sum_{n=1}^N w_n I(x_{ni} \!\ne\! 0, x_{nj} \!\ne\! 0) & q_{ijab} = q(x_i \eq a, x_j \eq b) :=& \frac{1}{N_{ij}} \sum_{n=1}^N w_n I(x_{ni} \eq a, x_{nj} \eq b) \end{align}\]

with $w_n$ being sequence weights calculated as described in methods section 2.6.3. With this definition, empirical amino acid frequencies are normalized without gaps, so that

\[\begin{equation} \sum_{a=1}^{20} q_{ia} = 1 \; , \; \sum_{a,b=1}^{20} q_{ijab} = 1. \tag{3.7} \end{equation}\]

3.7.3 The Regularized Full Log Likelihood and its Gradient With Gap Treatment

In pseudo-likelihood based methods, a regularisation is commonly used that can be interpreted to arise from a prior probability. The same treatment will be applied to the full likelihood. Gaussian priors $\mathcal{N}( \v | \v^*, \lambda_v^{-1} \I)$ and $\mathcal{N}( \w |\boldsymbol 0, \lambda_w^{-1} \I)$ will be used to constrain the parameters $\v$ and $\w$ and to fix the gauge. The choice of $v^*$ is discussed in section 3.7.4. By including the logarithm of this prior into the log likelihood the regularised log likelihood is obtained,

\[\begin{equation} \LLreg(\v,\w) = \log \left[ p(\X | \v,\w) \; \Gauss (\v | \v^*, \lambda_v^{-1} \I) \; \Gauss( \w | \boldsymbol 0, \lambda_w^{-1} \I) \right] \end{equation}\]

or explicitely,

\[\begin{align} \LLreg(\v,\w) =& \sum_{n=1}^N \left[ \sum_{i=1}^L v_i(x_{ni}) + \sum_{1\le i<j\le L} w_{ij}(x_{ni},x_{nj}) - \log Z_n(\v,\w) \right] \nonumber\\ & - \frac{\lambda_v}{2} \!\! \sum_{i=1}^L \sum_{a=1}^{20} (\via - \via^*)^2 - \frac{\lambda_w}{2} \sum_{1 \le i < j \le L} \sum_{a,b=1}^{20} \wijab^2 . \end{align}\]

The gradient of the regularized log likelihood has single components

\[\begin{align} \frac{\partial \LLreg}{\partial \via} =& \sum_{n=1}^N I(x_{ni}=a) - \sum_{n=1}^N \frac{\partial}{\partial \via} \, \log Z_n(\v,\w) - \lambda_v (\via - \via^*) \nonumber\\ =& \; N_i q(x_i \eq a) \nonumber\\ & - \sum_{n=1}^N \sum_{\mathbf{y} \in \Sn} \frac{ \exp \left( \sum_{i=1}^L v_i(y_i) + \sum_{1 \le i<j \le L}^L w_{ij}(y_i,y_j) \right) }{Z_n(\v,\w)} I(y_i=a) \nonumber\\ & - \lambda_v (\via - \via^*) \tag{3.8} \end{align}\]

and pair components

\[\begin{align} \frac{\partial \LLreg}{\partial \wijab} =& \sum_{n=1}^N I(x_{ni} \eq a, x_{nj} \eq b) - \sum_{n=1}^N \frac{\partial}{\partial \wijab} \log Z_n(\v,\w) - \lambda_w \wijab \nonumber\\ =& \; N_{ij} q(x_i \eq a, x_j=b) \nonumber\\ & - \sum_{n=1}^N \sum_{\mathbf{y} \in \Sn} \frac{ \exp \left( \sum_{i=1}^L v_i(y_i) + \sum_{1 \le i<j \le L}^L w_{ij}(y_i,y_j) \right) }{Z_n(\v,\w)} I(y_i \eq a, y_j \eq b) \nonumber\\ & - \lambda_w \wijab \tag{3.9} \end{align}\]

Note that (without regulariation $\lambda_v = \lambda_w = 0$) the empirical frequencies $q(x_i \eq a)$ and $q(x_i \eq a, x_j=b)$ are equal to the model probabilities at the maximum of the likelihood when the gradient becomes zero.

If the proportion of gap positions in $\X$ is small (e.g. $<5\%$, also compare percentage of gaps in dataset in Appendix Figure C.2), the sums over $\mathbf{y} \in \Sn$ in eqs. (3.8) and (3.9) can be approximated by $p(x_i=a | \v,\w) I(x_{ni} \ne 0)$ and $p(x_i=a, x_j=b | \v,\w) I(x_{ni} \ne 0, x_{nj} \ne 0)$, respectively, and the partial derivatives become

\[\begin{equation} \frac{\partial \LLreg}{\partial \via} = \; N_i q(x_i \eq a) - N_i \; p(x_i \eq a | \v,\w) - \lambda_v (\via - \via^*) \tag{3.10} \end{equation}\] \[\begin{equation} \frac{\partial \LLreg}{\partial \wijab} = \; N_{ij} q(x_i \eq a, x_j=b) - N_{ij} \; p(x_i \eq a, x_j \eq b | \v,\w) - \lambda_w \wijab \tag{3.11} \end{equation}\]

Note that the couplings between columns $i$ and $j$ in the hypothetical MSA presented in the last section 3.7.2 will now vanish since $N_{ij} \eq 0$ and the gradient with respect to $\wijab$ is equal to $-\lambda_w \wijab$.

3.7.4 The prior on single potentials

Most previous approaches chose a prior around the origin, $p(\v) = \Gauss ( \v| \mathbf{0}, \lambda_v^{-1} \I)$, i.e., $\via^* \eq 0$. It can be shown that the choice $\via^* \eq 0$ leads to undesirable results. Taking the sum over $b=1,\ldots, 20$ at the optimum of the gradient of couplings in eq. (3.11), yields

\[\begin{equation} 0 = N_{ij}\, q(x_i \eq a, x_j \ne 0) - N_{ij}\, p(x_i \eq a | \v, \w) - \lambda_w \sum_{b=1}^{20} \wijab \; , \tag{3.12} \end{equation}\]

for all $i,j \in \{1,\ldots,L\}$ and all $a \in \{1,\ldots,20\}$.

Note, that by taking the sum over $a=1,\ldots, 20$ it follows that, \[\begin{equation} \sum_{a,b=1}^{20} \wijab = 0. \tag{3.13} \end{equation}\]

At the optimum the gradient with respect to $\via$ vanishes and according to eq. (3.10), $p(x_i=a|\v,\w) = q(x_i=a) - \lambda_v (\via - \via^*) / N_i$. This term can be substituted into equation (3.12), yielding

\[\begin{equation} 0 = N_{ij} \, q(x_i \eq a, x_j \ne 0) - N_{ij} \, q(x_i=a) + \frac{N_{ij}}{N_i}\lambda_v (\via - \via^*) - \lambda_w \sum_{b=1}^{20} \wijab \; . \tag{3.14} \end{equation}\]

Considering a MSA without gaps, the terms $N_{ij} \, q(x_i \eq a, x_j \ne 0) - N_{ij} \, q(x_i=a)$ cancel out, leaving

\[\begin{equation} 0 = \lambda_v (\via - \via^*) - \lambda_w \sum_{b=1}^{20} \wijab . \tag{3.15} \end{equation}\] Now, consider a column $i$ that is not coupled to any other and assume that amino acid $a$ was frequent in column $i$ and therefore $\via$ would be large and positive. Then according to eq. (3.15), for any other column $j$ the 20 coefficients $\wijab$ for $b \in \{1,\ldots,20\}$ would have to take up the bill and deviate from zero! This unwanted behaviour can be corrected by instead choosing a Gaussian prior centered around $\v^*$ obeying \[\begin{equation} \frac{\exp(\via^*)}{\sum_{a^{\prime}=1}^{20} \exp(v_{ia^{\prime}}^*)} = q(x_i=a) . \end{equation}\]

This choice ensures that if no columns are coupled, i.e. $p(\seq | \v,\w) = \prod_{i=1}^L p(x_i)$, $\v=\v^*$ and $\w= \mathbf{0}$ gives the correct probability model for the sequences in the MSA. Furthermore imposing the restraint $\sum_{a=1}^{20} \via \eq 0$ to fix the gauge of the $\via$ (i.e. to remove the indeterminacy), yields

\[\begin{align} \via^* = \log q(x_i \eq a) - \frac{1}{20} \sum_{a^{\prime}=1}^{20} \log q(x_i \eq a^{\prime}) . \tag{3.16} \end{align}\]

For this choice, $\via - \via^*$ will be approximately zero and will certainly be much smaller than $\via$, hence the sum over coupling coefficients in eq. (3.15) will be close to zero, as it should be.

3.7.5 Stochastic Gradien Descent

The couplings $\wijab$ are initialized at 0 and single potentials $\vi$ will not be optimized but rather kept fixed at their maximum-likleihood estimate $\vi^*$ as described in methods section 3.7.4. The optimization is stopped when a maximum number of 5000 iterations has been reached or when the relative change over the L2-norm of parameter estimates, $||\w||_2$, over the last five iterations falls below the threshold of $\epsilon = 1e-8$. The gradient of the full likelihood is approximated with CD which involves Gibbs sampling of protein sequences according to the current model parametrization and is described in detail in methods section 3.7.6. Zero centered L2-regularization is used to constrain the coupling parameters $\w$ using the regularization coefficient $\lambda_w = 0.2L$ which is the default setting for optimizing the pseudo-likelihood with CCMpredPy. Performance will be evaluated by the mean precision of top ranked contact predictions over a validation set of 300 proteins, that is a subset of the data set described in methods section 2.6.1. Contact scores for couplings are computed as the APC corrected Frobenius norm as explained in section 1.2.4.6. Pseudo-likelihood couplings are computed with the tool CCMpredPy that is introduced in methods section 2.6.2 and the pseudo-likelihood contact score will serve as general reference method for tuning the hyperparameters.

3.7.5.1 The adaptive moment estimation optimizer ADAM Optimizer

ADAM [211] stores an exponentially decaying average of past gradients and squared gradients,

\[\begin{align} m_t &= \beta_1 m_{t−1} + (1 − \beta_1) g \\ v_t &= \beta_2 v_{t−1} + (1 − \beta_2) g^2 \; , \end{align}\]

with $g = \nabla_w \LLreg(\v^*,\w)$ and the rate of decay being determined by hyperparameters $\beta_1$ and $\beta_2$. Both terms $m_t$ and $v_t$ represent estimates of the first and second moments of the gradient, respectively. The following bias correction terms compensates for the fact that the vectors $m_t$ and $v_t$ are both initialized at zero and therefore are biased towards zero especially at the beginning of optimization,

\[\begin{align} \hat{m_t} &= \frac{m_t}{1-\beta_1^t} \\ \hat{v_t} &= \frac{v_t}{1-\beta_2^t} \; . \end{align}\] Parameters are then updated using step size $\alpha$, a small noise term $\epsilon$ and the corrected moment estimates $\hat{m_t}$, $\hat{v_t}$, according to \[\begin{equation} x_{t+1} = x_t - \alpha \cdot \frac{\hat{m_t}}{\sqrt{\hat{v_t}} + \epsilon} \end{equation}\]

Kingma et al. proposed the default values $\beta_1=0.9$, $\beta_2=0.999$ and $\epsilon=1e−8$ and a constant learning rate $\alpha=1e-3$ [211].

3.7.6 Computing the Gradient with Contrastive Divergence

This section describes the implementation details for approximating the gradient of the full likelihood with CD.

The gradient of the full log likelihood with respect to the couplings $\w$ is computed as the difference of paiwise amino acid counts between the input alignment and a sampled alignment plus an additional regularization term as given in eq. (3.1). Pairwise amino acid counts are computed from the input alignment accounting for sequence weights (described in methods section 2.6.3) and including pseudo counts (described in methods section 2.6.4). Pairwise amino acid counts for the sampled alignment are computed in the same way using the same sequence weights that have been computed for the input alignment. A subset of sequences of size $S \eq \min(10L, N)$, with $L$ being the length of sequences and $N$ the number of sequences in the input alignment, is randomly selected from the input alignment and used to initialize the Markov chains for the Gibbs sampling procedure. Consequently, the input MSA is bigger than the sampled MSA whenever there are more than $10L$ sequences in the input alignment. In that case, the weighted pairwise amino acid counts of the sampled alignment need to be rescaled such that the total sample counts match the total counts from the input alignment.

During the Gibbs sampling process, every position in every sequence will be sampled $K$ times (default $K\eq1$), according to the conditional probabilties given in eq. (3.2). The sequence positions will be sampled in a random order to prevent position bias. Gap positions will not be sampled, because Dr. Stefan Seemayer showed that sampling gap positions leads to artefacts in the contat maps (not published). For PCD a copy of the input alignment is generated at the beginning of optimization that will keep the persistent Markov chains and that will be updated after the Gibbs sampling procedure. The default Gibbs sampling procedure is outlined in the following pseudo-code:

# Input: multiple sequence alignment X  with N sequences of length L
# Input: model parameters v and w

N = dim(X)[0]     # number of sequences in alignment
L = dim(X)[1]     # length of sequences in alignment
S = min(10L, N)   # number of sequences that will be sampled
K = 1             # number of Gibbs steps

# randomly select S sequences from the input alignment X without replacement
sequences = random.select.rows(X, size=S, replace=False)

for seq in sequences:
    # perform K steps of Gibbs sampling
    for step in range(K):
        # iterate over permuted sequence positions i in {1, ..., L}
        for i in shuffle(range(L)):
            # ignore gap positions
            if seq[i] == gap:
              continue
            # compute conditional probabilities for every 
            # amino acid a in {1, ..., 20}
            for a in range(20):
              p_cond[a] = p(seq[i]=a | seq/i, v, w)
            # randomly select a new amino acid 
            # a in {1, ..., 20} for position i 
            # according to conditional probabilities
            seq[i] = random.integer({1, ...,20}, p_cond)

# sequences will now contain S newly sampled sequences
return sequences

References

211. Kingma, D., and Ba, J. (2014). Adam: A Method for Stochastic Optimization.