1.2 Introduction to Contact Prediction

Contact prediction refers to the prediction of physical contacts between amino acid side chains in the 3D protein structure, given the protein sequence as input.

Historically, contact prediction was motivated by the idea that compensatory mutations between spatially neighboring residues can be traced down from evolutionary records [46]. As proteins evolve, they are under selective pressure to maintain their function and correspondingly their structure. Consequently, residues and interactions between residues constraining the fold, protein complex formation, or other aspects of function are under selective pressure. Highly constrained residues and interactions will be strongly conserved [47]. Another possibility to maintain structural integrity is the mutual compensation of unbeneficial mutations. For example, the unfavourable mutation of a small amino acid residue into a bulky residue in the densely packed protein core might have been compensated in the course of evolution by a particularly small side chain in a neighboring position. Other physico-chemical quantities such as amino acid charge or hydrogen bonding capacity can also induce compensatory effects[48]. The MSA of a protein family comprises homolog sequences that have descended from a common ancestor and are aligned relative to each other. According to the hypothesis, compensatory mutations show up as correlations between the amino acid types of pairs of MSA columns and can be used to infer spatial proximity of residue pairs (see Figure 1.3).

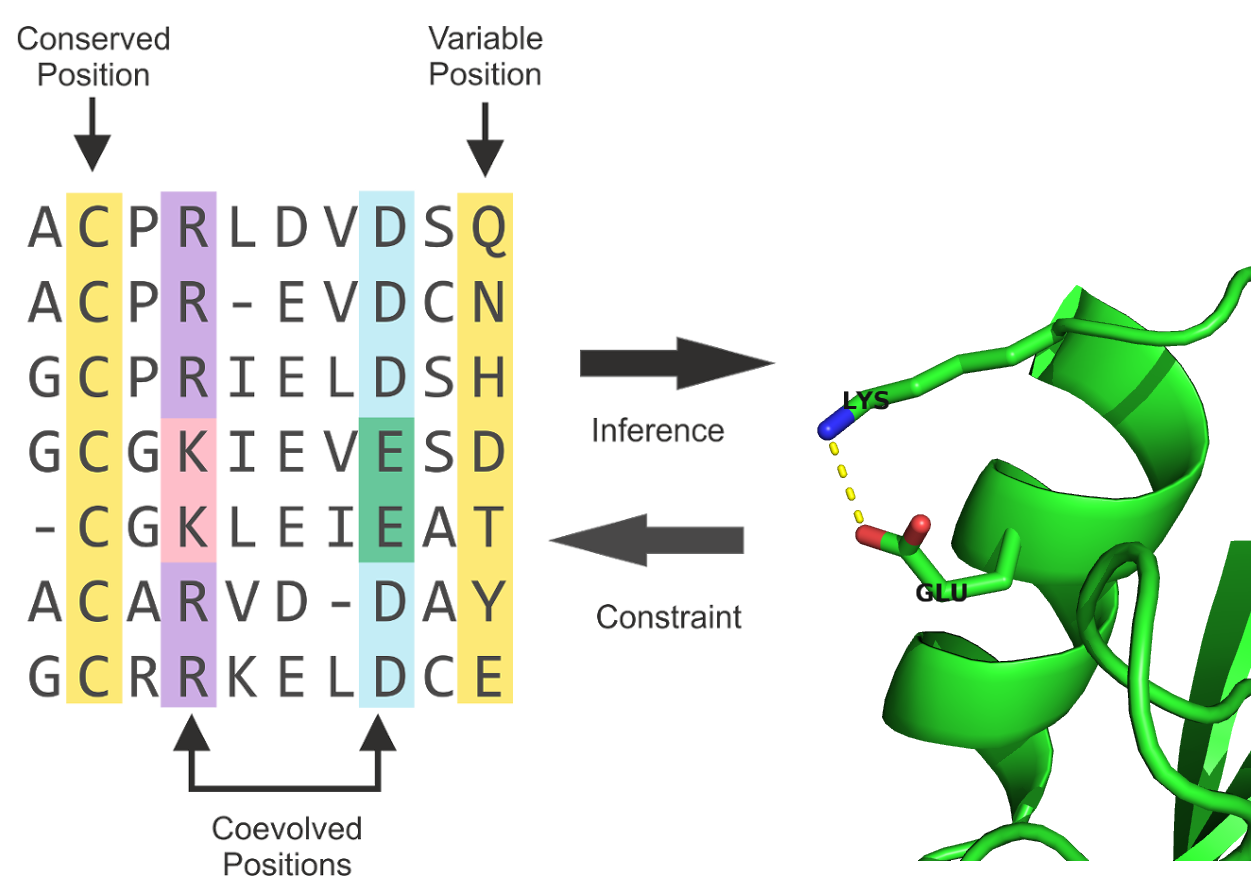
Figure 1.3: The evolutionary record of a protein family reveals evidence of compensatory mutations between spatially neighboring residues that are under selective pressure with respect to some physico-chemical constraints. Mining protein family sequence alignments for residue pairs with strong coevolutionary signals using statistical methods allows inference of spatial proximity for these residue pairs.

The following sections will give an overview over important methods and developments in the field of contact prediction.

1.2.1 Local Statistical Models

Early contact prediction methods used local pairwise statistics to infer contacts that regard pairs of amino acids in a sequence as statistically independent from another.

Several of these methods use correlation coefficient based measures, such as Pearson correlation between amino acid counts, properties associated with amino acids or mutational propensities at the sites of a MSA [46,48–51].

Many methods have been developed that are rooted in information theory and use MI measures to describe the dependencies between sites in the alignment [52–54]. Phylogenetic and entropic biases have been identified as strong sources of noise that confound the true coevolution signal [54–56]. Different variants of MI based approaches address these effects and improve on the signal-to-noise ratio [55,57,58]. The most prominent correction for background noises is APC that is still used by many modern methods and is discussed in section 1.2.4.6 [59]. Another popular method is OMES that essentially computes a chi-squared statistic to detect the differences between observed and expected pairwise amino acid frequencies for a pair of columns [60,61].

The traditional covariance approaches suffered from high false positive rates because of their inability to cope with transitive effects that arise from chains of correlations between multiple residue pairs [38,62,63]. The concept of transitve effects is illustrated in Figure 1.4. Considering three residues A, B and C, where A physically interacts with B and B with C. Strong statistical dependencies between pairs (A,B) and (B,C) can induce strong indirect signals for residues A and C, eventhough they are not physically interacting. These indirect correlations can become even larger than signals of other directly interacting pairs (D,E) and thus lead to false predictions [63].

Local statistical methods consider residue pairs independent of one another which is why they cannot distinguish between direct and indirect correlation signals. In contrast, global statistical models presented in the next section learn a joint probability distribution over all residues allowing to disentangle transitive effects [38,63]. Eventhough local statistical methods cannot compete with modern predictors, OMES and MI based scores often serve as a baseline in performance benchmarks for contact prediction [64,65].

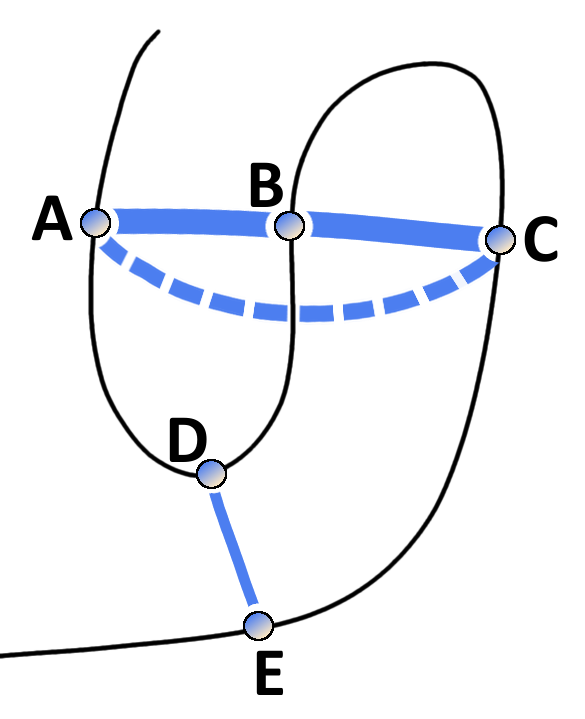
Figure 1.4: Effects of chained covariation obscure signals from true physical interactions. Consider residues A through E with physical interactions between the residue pairs A-B, B-C and D-E. The thickness of blue lines between residues reflects the strength of statistical dependencies between the corresponding alignment columns. Strong statistical dependencies between residue pairs (A,B) and (B,C) can induce a strong dependency between the spatially distant residues A and C. Covariation signals arising from transitive effects can become even stronger than other direct covariation signals and lead to false positive predictions.

1.2.2 Global Statistical Models

A huge leap forward was the development of sophisticated statistical models that make predictions for a single residue pair while considering all other pairs in the protein. These global models allow for the distinction between transitive and causal interactions which has been referred to in the literature as DCA [38,62].

In 1999 Lapedes et al. were the first to propose a global statistical approach for the prediction of residue-residue contacts in order to disentangle transitive effects [62]. They consider a Pott’s model that can be derived under a maximum entropy assumption and use the model specific coupling parameters to infer interactions. At that time the wider implications of this advancement went unnoted, but meanwhile the Pott’s Model has become the most prominent statistical model for contact prediction. Section 1.2.4 deals extensively with the derivation and properties of the Pott’s model, its application to contact prediction and its numerous realizations.

A global statistical model not motivated by the maximum entropy approach was proposed by Burger and Nijmwegen in 2010 [63,66]. Their fast Bayesian network model incorporates additional prior information and phylogenetic correction via APC but cannot compete with the pseudo-likelihood approaches presented in section 1.2.4.5.

1.2.3 Machine Learning Methods and Meta-Predictors

With the steady increase in protein sequence data, machine learning based methods have emerged that extract features from MSAs in order to learn associations between input features and residue-residue contacts. Sequence features typically include predicted solvent accessibility, predicted secondary structure, contact potentials, conservation scores, global protein features, pairwise coevolution statistics and averages of certain features over sequence windows. Numerous sequence-based methods have been developed using machine learning algorithms, such as support support vector machines (SVMCon [67], SVM-SEQ [68]), random forests (ProC_S3 [69], TMhhcp [70], PhyCMap [71]), neural networks (NETCSS [72], SAM [73], [74], SPINE-2D [75], NNCon [76]) deep neural networks (DNCon [77], CMAPpro [78]) and ensembles of genetic algorithm classfiers (GaC [79]).

Different contact predictors, especially when rooted in distinct principles like sequence-based and coevolution methods, provide orthogonal information on the likelihood that a pair of residues makes a contact [67,80]. The next logical step in method development therefore constitutes the combination of several base predictors and classical sequence-derived features in the form of meta-predictors.

The first published meta-predictor was PconsC in 2013, combining sequence features and predictions from the coevolution methods PSICOV and plmDCA [81]. In a follow-up version PSICOV has been replaced with gaussianDCA and the sequence-based method PhyCMap [82]. EPC-MAP was published in 2014 integrating GREMLIN as a coevolution feature with physicochemical information from predicted ab initio protein structures [83]. In 2015, MetaPSICOV was released combining predictions from PSICOV, mfDCA and CCMpred with other sequence derived feautures [84]. RaptorX uses CCMpred as coevolution feature and other standard contact prediction features within an ultra-deep neural network [85]. The newest developments EPSILON-CP and NeBcon both comprise the most comprehensive usage of contact prediction methods so far, combining five and eight state-of-the-art contact predictors, respectively [86,87].

Another conceptual advancement besides the combination of sources of information is based on the fact that contacts are not randomly or independently distributed. DiLena and colleagues found that over 98% of long-range contacts (sequence separation > 24 positions) are in close proximity of other contacts, compared to 30% for non-contacting pairs [78]. The distribution of contacts is governed by local structural elements, like interactions between helices or \(\beta\)-sheets, leading to characteristic patterns in the contact map that can be recognised [88]. Deep learning provides the means to model higher level abstractions of data and several methods apply multi-layered algorithms to refine predictions by learning patterns that reflect the local neighborhood of a contact [78,84,85,89].

Eventhough a benchmark comparing the recently developed meta-predictors is yet to be made, it becomes clear from the recent CASP experiments, that meta-predictors outperform pure coevolution methods [90]. As coevolution scores comprise the most informative feautures among the set of input features, it is clear that meta-predictors will benefit from further improvements of pure coevolution methods [85,86].

1.2.4 Modelling Protein Families with Potts Model

Infering contacts from a joint probability distribution over all residues in a protein sequence instead of using simple pairwise statistics has been proven to enable the distinction of direct statistical dependencies between residues from indirect dependencies mediated through other residues. The global statistical model that is commonly used to describe this joint probability distribution is the Potts model. It is a well-established model in statistical mechanics and can be derived from a maximum entropy assumption which is explained in the following.

The principle of maximum entropy, proposed by Jaynes in 1957 [91,92], states that the probability distribution which makes minimal assumptions and best represents observed data is the one that is in agreement with measured constraints (prior information) and has the largest entropy. In other words, from all distributions that are consistent with measured data, the distribution with maximal entropy should be chosen.

A protein family is represented by a MSA \(\X = \{ \seq_1, \ldots, \seq_N \}\) of \(N\) protein sequences. Every protein sequence of the protein family represents a sample drawn from a target distribution \(p(\seq)\), so that each protein sequence is associated with a probability. Each sequence \(\seq_n = (\seq_{n1}, ..., \seq_{nL})\) is of length \(L\) and every position constitutes a categorical variable \(x_{i}\) that can take values from an alphabet indexed by \(\{0, ..., 20\}\), where 0 stands for a gap and \(\{1, ... , 20\}\) stand for the 20 types of amino acids. The measured constraints are given by the empirically observed single and pairwise amino acid frequencies that can be calculated as

\[\begin{equation} f_i(a) = f(x_i\eq a) = \frac{1}{N}\sum_{n=1}^N I(x_{ni} \eq a) \; , \end{equation}\] \[\begin{equation} f_{ij}(a,b) = f(x_i\eq a, x_j\eq b) = \frac{1}{N} \sum_{n=1}^N I(x_{ni} \eq a, x_{nj} \eq b) \; . \tag{1.1} \end{equation}\]

According to the maximum entropy principle, the distribution \(p(\seq)\) should have maximal entropy and reproduce the empirically observed amino acid frequencies, so that

\[\begin{align} f(x_i\eq a) &\equiv p(x_i\eq a) \nonumber\\ &= \sum_{\seq\prime_1, \ldots, \seq\prime_L = 1}^{q} p(x\prime) I(x\prime_i \eq a) \\ f(x_i\eq a, x_j\eq b) &\equiv p(x_i\eq a, x_j \eq b) \nonumber \\ &= \sum_{\seq\prime_1, \ldots, \seq\prime_L = 1}^{q} p(x\prime) I(x\prime_i\eq a, x\prime_j \eq b) \; . \tag{1.2} \end{align}\]

Solving for the distribution \(p(\seq)\) that maximizes the Shannon entropy \(S= -\sum_{\seq\prime} p(\seq\prime) \log p(\seq\prime)\) while satisfying the constraints given by the empircial amino acid frequencies in eq. (1.2) by introducing Lagrange multipliers \(\wij\) and \(\vi\), results in the formulation of the Potts model,

\[\begin{equation} p(\seq | \v, \w ) = \frac{1}{Z(\v, \w)} \exp \left( \sum_{i=1}^L v_i(x_i) \sum_{1 \leq i < j \leq L}^L w_{ij}(x_i, x_j) \right) \; . \tag{1.3} \end{equation}\]

The Lagrange multipliers \(\wij\) and \(\vi\) remain as model parameters to be fitted to data. \(Z\) is a normalization constant also known as partition function that ensures the total probabilty adds up to one by summing over all possible assignments to \(\seq\),

\[\begin{equation} Z(\v, \w) = \sum_{\seq\prime_1, \ldots, \seq\prime_L = 1}^{q} \exp \left( \sum_{i=1}^L v_i(x_i) \sum_{1 \leq i < j \leq L}^L w_{ij}(x_i, x_j) \right) \; . \tag{1.4} \end{equation}\]

1.2.4.1 Model Properties

The Potts model is specified by singlet terms \(\via\) which describe the tendency for each amino acid a to appear at position \(i\), and pair terms \(\wijab\), also called couplings, which describe the tendency of amino acid a at position \(i\) to co-occur with amino acid b at position \(j\). In contrast to mere correlations, the couplings explain the causative dependence structure between positions by jointly modelling the distribution of all positions in a protein sequence and thus account for transitive effects. By doing so, a major source of noise in contact prediction methods is eliminated.

To get some intuition for the coupling coefficients, note that \(\wijab = 1\) corresponds to a 2.7-fold higher probability for a and b to occur together than what is expected from the singlet frequencies if a and b were independent. Pairs of residues that are not in contact tend to have negligable couplings, \(\wij \approx 0\), whereas pairs in contact tend to have vectors significantly different from 0. For contacting residues \(i\) and \(j\) in real world MSAs typical coupling strengths are on the order of \(||\wij || \approx 0.1\) (regularization dependent).

Maximum entropy models naturally give rise to exponential family distributions that express useful properties for statistical modelling, such as the convexity of the likelihood function which consequently has a unique, global minimum [93,94].

The Potts model is a discrete instance of what is referred to as a pairwise Markov random field in the statistics community. MRFs belong to the class of undirected graphical models, that represent the probability distribution in terms of a graph with nodes and edges characterizing the variables and the dependence structure between variables, respectively.

1.2.4.2 Gauge Invariance

As every variable \(x_{ni}\) can take \(q=21\) values, the model has \(L \! \times \! q + L(L-1)/2 \! \times \! q^2\) parameters. But the parameters are not uniquely determined and multiple parametrizations yield identical probability distributions.

For example, adding a constant to all elements in \(v_i\) for any fixed position \(i\) or similarly adding a constant to \(\via\) for any fixed position \(i\) and amino acid \(a\) and subtracting the same constant from the \(qL\) coefficients \(\wijab\) with \(b \in \{1, \ldots, q\}\) and \(j \in \{1, \ldots, L \}\) leaves the probabilities for all sequences under the model unchanged, since such a change will be compensated by a change of \(Z(\v, \w)\) in eq. (1.4).

The overparametrization is referred to as gauge invariance in statistical physics literature and can be eliminated by removing parameters [38,95]. An appropriate choice of which parameters to remove, referred to as gauge choice, reduces the number of parameters to \(L \! \times \! (q-1) + L(L-1)/2 \! \times \! (q-1)^2\). Popular gauge choices are the zero-sum gauge or Ising-gauge used by Weigt et al. [38] imposed by the restraints,

\[\begin{equation} \sum_{a=1}^{q} v_{ia} = \sum_{a=1}^{q} \wijab = \sum_{a=1}^{q} w_{ijba} = 0 \tag{1.5} \end{equation}\]

for all \(i,j,b\) or the lattice-gas gauge used by Morcos et al [95] and Marks et al [39] imposed by restraints

\[\begin{equation} \wij(q,a) = \wij(a,q) = \vi(q) = 0 \tag{1.6} \end{equation}\]

for all \(i,j,a\) [96].

Alternatively, the indeterminacy can be fixed by including a regularization prior (see next section). The regularizer selects for a unique solution among all parametrizations of the optimal distribution and therefore eliminates the need to choose a gauge [97–99].

1.2.4.3 Inferring Parameters for the Potts Model

Typically, parameter estimates are obtained by maximizing the log-likelihood function of the parameters over observed data. For the Potts model, the log-likelihood function is computed over sequences in the alignment \(\mathbf{X}\):

\[\begin{align} \text{LL}(\v, \w | \mathbf{X}) =& \sum_{n=1}^N \log p(\seq_n) \nonumber\\ =& \sum_{n=1}^N \left[ \sum_{i=1}^L v_i(x_{ni}) + \sum_{1 \leq i < j \leq L}^L w_{ij}(x_{xn}, x_{nj}) - \log Z \right] \tag{1.7} \end{align}\]

The number of parameters in a Potts model is typically larger than the number of observations, i.e. the number of sequences in the MSA. Considering a protein of length \(L=100\), there are approximately \(2 \times 10^6\) parameters in the model whereas the largest protein families comprise only around \(10^5\) sequences (see Figure 1.11). An underdetermined problem like this renders the use of regularizers neccessary in order to prevent overfitting.

Typically, an L2-regularization is used that pushes the single and pairwise terms smoothly towards zero and is equivalent to the logarithm of a zero-centered Gaussian prior,

\[\begin{align} R(\v, \w) &= \log \left[ \mathcal{N}(\v | \mathbf{0}, \lambda_v^{-1} I) \mathcal{N}(\w | \mathbf{0}, \lambda_w^{-1} I) \right] \nonumber \\ &= -\frac{\lambda_v}{2} ||\v||_2^2 - \frac{\lambda_w}{2} ||\w||_2^2 + \text{const.} \; , \tag{1.8} \end{align}\]

where the strength of regularization is tuned via the regularization coefficients \(\lambda_v\) and \(\lambda_w\) [100–102].

However, optimizing the log-likelihood requires computing the partition function \(Z\) given in eq. (1.4) that sums \(q^L\) terms. Computing this sum is intractable for realistic protein domains with more than 100 residues. Consequently, evaluating the likelihood function at each iteration of an optimization procedure is infeasible due to the exponential complexity of the partition function in protein length \(L\).

Many approximate inference techniques have been developed to sidestep the infeasible computation of the partition function for the specific problem of predicting contacts that are briefly explained in the next section.

1.2.4.4 Solving the Inverse Potts Problem

In 1999 Lapedes et al. were the first to propose maximum entropy models for the prediction of residue-residue contacts in order to disentangle transitive effects [62]. In 2002 they applied their idea to 11 small proteins using an iterative Monte Carlo procedure to obtain estimates of the model parameters and achieved an increase in accuracy of 10-20% compared to the local statistical models [103]. As the calculations involved were very time-consuming and at that time required supercomputing resources, the wider implications were not noted yet.

Ten years later Weight et al proposed an iterative message-passing algorithm, here referred to as mpDCA, to approximate the partition function [38]. Eventhough their approach is computationally very expensive and in practice only applicable to small proteins, they obtained remarkable results for the two-component signaling system in bacteria.

Balakrishnan et al were the first to apply pseudo-likelihood approximations to the full likelihood in 2011 [104]. The pseudo-likelihood optimizes a different objective and replaces the global partition function \(Z\) with local estimates. Balakrishnan and colleagues applied their method GREMLIN to learn sparse graphical models for 71 protein families. In a follow-up study in 2013, the authors proposed an improved version of GREMLIN that uses additional prior information [102].

Also in 2011, Morcos et al. introduced a naive mean-field inversion approximation to the partition function, named mfDCA [95]. This method allows for drastically shorter running times as the mean-field approach boils down to inverting the empirical covariance matrix calculated from observed amino acid frequencies for each residue pair \(i\) and \(j\) of the alignment. This study performed the first high-throughput analysis of intradomain contacts for 131 protein families and facilitated the prediction of protein structures from accurately predicted contacts in [39].

The initial work by Balakrishnan and collegueas went almost unnoted as it was not primarily targeted to the problem of contact prediction. Ekeberg and collegueas independently developed the pseudo-likelihood method plmDCA in 2013 and showed its superior precision over mfDCA [98].

A related approach to mean-field approximation is sparse inverse covariance estimation, named PSICOV, developed by Jones et al. (2012) [65]. PSICOV uses an L1-regularization, known as graphical Lasso, to invert the correlation matrix and learn a sparse graphical model [105]. Both procedures, mfDCA and PSICOV, assume the model distribution to be a multivariate Gaussian. It has been shown by Banerjee et al. (2008)that this dual optimization solution also applies to binary data, as is the case in this application, where each position is encoded as a 20-dimensional binary vector [106].

Another related approach to mfDCA and PSICOV is gaussianDCA, proposed in 2014 by Baldassi et al. [107]. Similar to the other both approaches, they model the data as multivariate Gaussian but within a simple Bayesian formalism by using a suitable prior and estimating parameters over the posterior distribution.

So far, pseudo-likelihood has proven to be the most successful approximation of the likelihood with respect to contact prediction performance. Currently, there exist several implementations of pseudo-likelihood maximization that vary in slight details, perform similarly and thus are equally popular in the community, such as CCMpred [100], plmDCA[101] and GREMLIN [102].

1.2.4.5 Maximum Likelihood Inference for Pseudo-Likelihood

The pseudo-likelihood is a rather old estimation principle that was suggested by Besag already in 1975 [108]. It represents a different objective function than the full likelihood and approximates the joint probability with the product over conditionals for each variable, i.e. the conditional probability of observing one variable given all the others:

\[\begin{align} p(\seq | \v,\w) \approx& \prod_{i=1}^L p(x_i | \seq_{\backslash xi}, \v,\w) \nonumber \\ =& \prod_{i=1}^L \frac{1}{Z_i} \exp \left( v_i(x_i) \sum_{1 \leq i < j \leq L}^L w_{ij}(x_i, x_j) \right) \end{align}\]

Here, the normalization term \(Z_i\) sums only over all assignments to one position \(i\) in sequence:

\[\begin{equation} Z_i = \sum_{a=1}^{q} \exp \left( v_i(a) \sum_{1 \leq i < j \leq L}^L w_{ij}(a, x_j) \right) \tag{1.9} \end{equation}\]

Replacing the global partition function in the full likelihood with local estimates of lower complexity in the pseudo-likelihood objective resolves the computational intractability of the parameter optimization procedure. Hence, it is feasible to maximize the pseudo-log-likelihood function,

\[\begin{align} \text{pLL}(\v, \w | \mathbf{X}) =& \sum_{n=1}^N \sum_{i=1}^L \log p(x_i | \seq_{\backslash xi}, \v,\w) \nonumber \\ =& \sum_{n=1}^N \sum_{i=1}^L \left[ v_i(x_{ni}) + \sum_{j=i+1}^L w_{ij}(x_{ni}, x_{nj}) - \log Z_{ni} \right] \;, \end{align}\]

plus an additional regularization term in order to prevent overfitting and to fix the gauge to arrive at a MAP estimate of the parameters,

\[\begin{equation} \hat{\v}, \hat{\w} = \underset{\v, \w}{\operatorname{argmax}} \; \text{pLL}(\v, \w | \mathbf{X}) + R(\v, \w) \; . \end{equation}\]

Eventhough the pseudo-likelihood optimizes a different objective than the full-likelihood, it has been found to work well in practice for many problems, including contact prediction [94,97–99]. The pseudo-likelihood function retains the concavity of the likelihood and it has been proven to be a consistent estimator in the limit of infinite data for models of the exponential family [97,108,109]. That is, as the number of sequences in the alignment increases, pseudo-likelihood estimates converge towards the true full likelihood parameters.

1.2.4.6 Computing Contact Maps

Model inference as described in the last section yields MAP estimates of the couplings \(\hat{\w}_{ij}\). In order to obtain a scalar measure for the coupling strength between two residues \(i\) and \(j\), all available methods presented in section 1.2.4.4 heuristically map the \(21 \! \times \! 21\) dimensional coupling matrix \(\wij\) to a single scalar quantity.

mpDCA [38] and mfDCA [39,95] employ a score called DI, that essentially computes the MI for two positions \(i\) and \(j\) using the couplings \(\wij\) instead of pairwise amino acid frequencies. Most pseudo-likelihood methods (plmDCA [98,101], CCMpred [100], GREMLIN [102]) compute the Frobenius norm of the coupling matrix \(\wij\) to obtain a scalar contact score \(C_{ij}\),

\[\begin{equation} C_{ij} = ||\wij||_2 = \sqrt{\sum_{a,b=1}^q \wijab^2} \; . \tag{1.10} \end{equation}\]

The Frobenius norm improves prediction performance over DI and further improvements can be obtained by computing the Frobenius norm only on the \(20 \times 20\) submatrix thus ignoring contributions from gaps [98,107,110]. PSICOV [65] uses an L1-norm on the \(20 \times 20\) submatrix instead of the Frobenius norm.

Furthermore it should be noted that the Frobenius norm is gauge dependent and is minimized by the zero-sum gauge [38]. Therefore, the coupling matrices should be transformed to zero-sum gauge before computing the Frobenius norm

\[\begin{equation} \w^{\prime}_{ij} = \wij - \wij(\cdot, b) - \wij(a, \cdot) + \wij(\cdot, \cdot) \; , \tag{1.11} \end{equation}\]

where \(\cdot\) denotes average over the respective indices [98,100,101,107].

Another commonly applied heuristic known as APC has been introduced by Dunn et al. in order to reduce background noise arising from correlations between positions with high entropy or phylogenetic couplings [59]. APC is a correction term that is computed from the raw contact map as the product over average row and column contact scores \(\overline{C_i}\) divided by the average contact score over all pairs \(\overline{C_{ij}}\). The corrected contact score \(C_{ij}^{APC}\) is obtained by subtracting the APC term from the raw contact score \(C_{ij}\),

\[\begin{equation} C_{ij}^{APC} = C_{ij} - \frac{\overline{C_i} \; \overline{C_j}}{\overline{C_{ij}}}\; . \tag{1.12} \end{equation}\]

Visually, APC creates a smoothing effect on the contact maps that is illustrated in Figure 1.5 and it has been found to substantially boost contact prediction performance [59,102]. It was first adopted by PSICOV [65] but is now used by most methods to adjust raw contact scores.

It was long under debate why APC works so well and how it can be interpreted. Zhang et al. showed that APC essentially approximates the first principal component of the contact matrix and therefore removes the highest variability in the matrix that is assumed to arise from background biases [111]. Furthermore, they studied an advanced decomposition technique, called LRS matrix decomposition, that decomposes the contact matrix into a low-rank and a sparse component, representing background noise and true correlations, respectively.
Inferring contacts from the sparse component works astonishing well, improving precision further over APC independent of the underlying statistical model.

Dr Stefan Seemayer could show that the main component of background noise can be attributed to entropic effects and that a substantial part of APC amounts to correcting for these entropic biases (unpublished). In his doctoral thesis, he developed an entropy correction, computed as the geometric mean of per-column entropies, that correlates well with the APC correction term and yields similar precision for predicted contacts. The entropy correction has the advantage that it is computed from input statistics and therefore is independent of the statistical model used to infer the couplings. In contrast, APC and other denoising techniques such as LRS [111] discussed above, estimate a background model from the final contact matrix, thus depending on the statistical model used to infer the contact matrix.

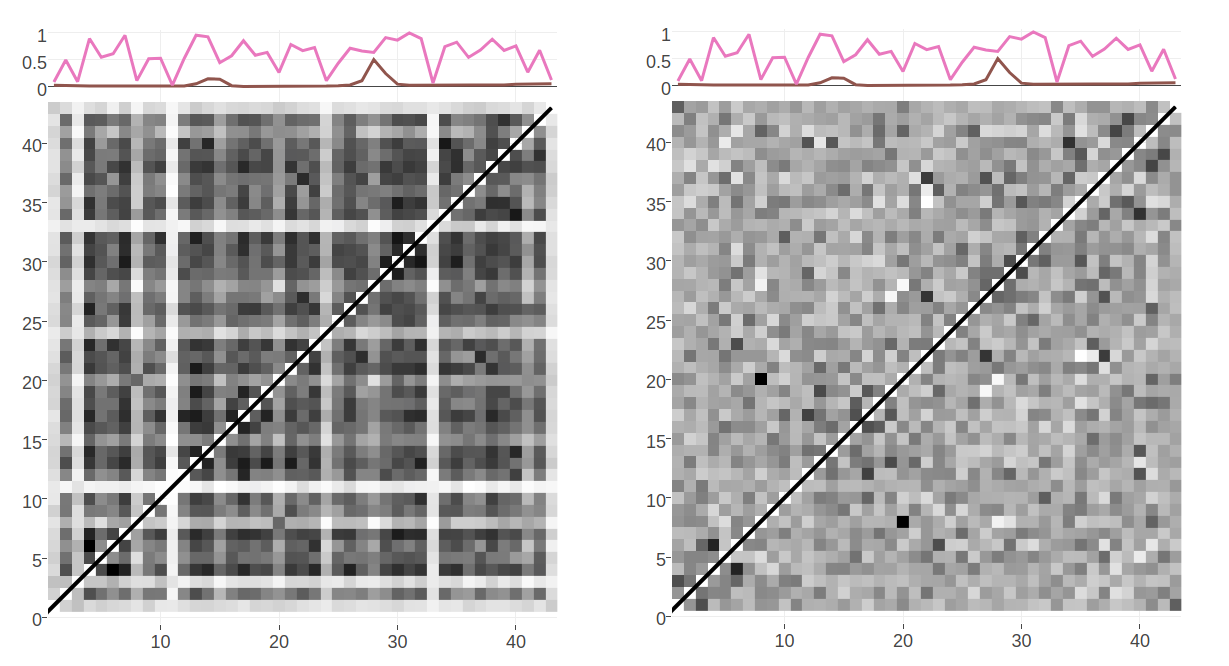
Figure 1.5: Contact maps computed from pseudo-likelihood couplings. Subplot on top of the contact maps illustrates the normalized Shannon entropy (pink line) and percentage of gaps for every position in the alignment (brown line). Left: Contact map computed with Frobenius norm as in eq. (1.10). Overall coupling values are dominated by entropic effects, i.e. the amount of variation for a MSA position, leading to striped brightness patterns. For example, positions with high column entropy (e.g. positions 7, 12 or 31) have higher overall coupling values than positions with low column entropy (e.g. positions 11, 24 or 33). b: previous contact map but corrected for background noise with the APC as in eq. (1.12).

References

46. Göbel, U., Sander, C., Schneider, R., and Valencia, A. (1994). Correlated mutations and residue contacts in proteins. Proteins 18, 309–317., doi: 10.1002/prot.340180402.

47. Godzik, A., and Sander, C. (1989). Conservation of residue interactions in a family of Ca-binding proteins. "Protein Eng. Des. Sel. 2, 589–596., doi: 10.1093/protein/2.8.589.

48. Neher, E. (1994). How frequent are correlated changes in families of protein sequences? Proc. Natl. Acad. Sci. U. S. A. 91, 98–102.

51. Shindyalov, I., Kolchanov, N., and Sander, C. (1994). Can three-dimensional contacts in protein structures be predicted by analysis of correlated mutations? "Protein Eng. Des. Sel. 7, 349–358., doi: 10.1093/protein/7.3.349.

52. Clarke, N.D. (1995). Covariation of residues in the homeodomain sequence family. Protein Sci. 4, 2269–78., doi: 10.1002/pro.5560041104.

54. Martin, L.C., Gloor, G.B., Dunn, S.D., and Wahl, L.M. (2005). Using information theory to search for co-evolving residues in proteins. Bioinformatics 21, 4116–24., doi: 10.1093/bioinformatics/bti671.

56. Fodor, A.A., and Aldrich, R.W. (2004). Influence of conservation on calculations of amino acid covariance in multiple sequence alignments. Proteins 56, 211–21.

55. Atchley, W.R., Wollenberg, K.R., Fitch, W.M., Terhalle, W., and Dress, A.W. (2000). Correlations Among Amino Acid Sites in bHLH Protein Domains: An Information Theoretic Analysis. Mol. Biol. Evol. 17, 164–178., doi: 10.1093/oxfordjournals.molbev.a026229.

57. Tillier, E.R., and Lui, T.W. (2003). Using multiple interdependency to separate functional from phylogenetic correlations in protein alignments. Bioinformatics 19, 750–755., doi: 10.1093/bioinformatics/btg072.

58. Gouveia-Oliveira, R., and Pedersen, A.G. (2007). Finding coevolving amino acid residues using row and column weighting of mutual information and multi-dimensional amino acid representation. Algorithms Mol. Biol. 2, 12., doi: 10.1186/1748-7188-2-12.

59. Dunn, S.D., Wahl, L.M., and Gloor, G.B. (2008). Mutual information without the influence of phylogeny or entropy dramatically improves residue contact prediction. Bioinformatics 24, 333–40., doi: 10.1093/bioinformatics/btm604.

60. Kass, I., and Horovitz, A. (2002). Mapping pathways of allosteric communication in GroEL by analysis of correlated mutations. Proteins 48, 611–7., doi: 10.1002/prot.10180.

61. Noivirt, O., Eisenstein, M., and Horovitz, A. (2005). Detection and reduction of evolutionary noise in correlated mutation analysis. Protein Eng. Des. Sel. 18, 247–53., doi: 10.1093/protein/gzi029.

38. Weigt, M., White, R.A., Szurmant, H., Hoch, J.A., and Hwa, T. (2009). Identification of direct residue contacts in protein-protein interaction by message passing. Proc. Natl. Acad. Sci. U. S. A. 106, 67–72., doi: 10.1073/pnas.0805923106.

62. Lapedes, A., Giraud, B., Liu, L., and Stormo, G. (1999). Correlated mutations in models of protein sequences: phylogenetic and structural effects. 33, 236–256.

63. Burger, L., and Nimwegen, E. van (2010). Disentangling direct from indirect co-evolution of residues in protein alignments. PLoS Comput. Biol. 6, e1000633., doi: 10.1371/journal.pcbi.1000633.

64. Juan, D. de, Pazos, F., and Valencia, A. (2013). Emerging methods in protein co-evolution. Nat. Rev. Genet. 14, 249–61., doi: 10.1038/nrg3414.

65. Jones, D.T., Buchan, D.W.A., Cozzetto, D., and Pontil, M. (2012). PSICOV: precise structural contact prediction using sparse inverse covariance estimation on large multiple sequence alignments. Bioinformatics 28, 184–90., doi: 10.1093/bioinformatics/btr638.

66. Burger, L., and Nimwegen, E. van (2008). Accurate prediction of protein-protein interactions from sequence alignments using a Bayesian method. Mol. Syst. Biol. 4, 165., doi: 10.1038/msb4100203.

67. Cheng, J., and Baldi, P. (2007). Improved residue contact prediction using support vector machines and a large feature set. BMC Bioinformatics 8., doi: 10.1186/1471-2105-8-113.

68. Wu, S., and Zhang, Y. (2008). A comprehensive assessment of sequence-based and template-based methods for protein contact prediction. Bioinformatics 24, 924–31.

69. Li, Y., Fang, Y., and Fang, J. (2011). Predicting residue-residue contacts using random forest models. Bioinformatics 27., doi: 10.1093/bioinformatics/btr579.

70. Wang, X.-F., Chen, Z., Wang, C., Yan, R.-X., Zhang, Z., and Song, J. (2011). Predicting residue-residue contacts and helix-helix interactions in transmembrane proteins using an integrative feature-based random forest approach. PLoS One 6, e26767., doi: 10.1371/journal.pone.0026767.

71. Wang, Z., and Xu, J. (2013). Predicting protein contact map using evolutionary and physical constraints by integer programming. Bioinformatics 29, i266–73.

72. Fariselli, P., Olmea, O., Valencia, A., and Casadio, R. (2001). Prediction of contact maps with neural networks and correlated mutations. Protein Eng. Des. Sel. 14, 835–843.

73. Shackelford, G., and Karplus, K. (2007). Contact prediction using mutual information and neural nets. Proteins 69 Suppl 8, 159–64., doi: 10.1002/prot.21791.

74. Hamilton, N., Burrage, K., Ragan, M.A., and Huber, T. (2004). Protein contact prediction using patterns of correlation. Proteins Struct. Funct. Bioinforma. 56, 679–684., doi: 10.1002/PROT.20160.

75. Xue, B., Faraggi, E., and Zhou, Y. (2009). Predicting residue-residue contact maps by a two-layer, integrated neural-network method. Proteins 76, 176–83.

76. Tegge, A.N., Wang, Z., Eickholt, J., and Cheng, J. (2009). NNcon: improved protein contact map prediction using 2D-recursive neural networks. Nucleic Acids Res. 37, W515–8.

77. Eickholt, J., and Cheng, J. (2012). Predicting protein residue–residue contacts using deep networks and boosting. 28, 3066–3072., doi: 10.1093/bioinformatics/bts598.

78. Di Lena, P., Nagata, K., and Baldi, P. (2012). Deep architectures for protein contact map prediction. Bioinformatics 28, 2449–57.

79. Chen, P., and Li, J. (2010). Prediction of protein long-range contacts using an ensemble of genetic algorithm classifiers with sequence profile centers. BMC Struct. Biol. 10 Suppl 1, S2., doi: 10.1186/1472-6807-10-S1-S2.

80. Jones, D.T., Singh, T., Kosciolek, T., and Tetchner, S. (2015). MetaPSICOV: combining coevolution methods for accurate prediction of contacts and long range hydrogen bonding in proteins. Bioinformatics 31, 999–1006., doi: 10.1093/bioinformatics/btu791.

81. Skwark, M.J., Abdel-Rehim, A., and Elofsson, A. (2013). PconsC: combination of direct information methods and alignments improves contact prediction. Bioinformatics 29, 1815–6.

82. Skwark, M.J., Michel, M., Menendez Hurtado, D., Ekeberg, M., and Elofsson, A. (2016). Accurate contact predictions for thousands of protein families using PconsC3. bioRxiv.

83. Schneider, M., and Brock, O. (2014). Combining Physicochemical and Evolutionary Information for Protein Contact Prediction. PLoS One 9, e108438.

84. Jones, D.T., Singh, T., Kosciolek, T., and Tetchner, S. (2015). MetaPSICOV: combining coevolution methods for accurate prediction of contacts and long range hydrogen bonding in proteins. Bioinformatics 31, 999–1006.

85. Wang, S., Sun, S., Li, Z., Zhang, R., and Xu, J. (2016). Accurate De Novo Prediction of Protein Contact Map by Ultra-Deep Learning Model. PLoS Comput. Biol. 13, e1005324., doi: 10.1371/journal.pcbi.1005324.

86. Stahl, K., Schneider, M., and Brock, O. (2017). EPSILON-CP: using deep learning to combine information from multiple sources for protein contact prediction. BMC Bioinformatics 18, 303., doi: 10.1186/s12859-017-1713-x.

87. He, B., Mortuza, S.M., Wang, Y., Shen, H.-B., and Zhang, Y. (2017). NeBcon: Protein contact map prediction using neural network training coupled with naïve Bayes classifiers. Bioinformatics., doi: 10.1093/bioinformatics/btx164.

88. Andreani, J., and Söding, J. (2015). Bbcontacts: Prediction of $$-strand pairing from direct coupling patterns. Bioinformatics 31, 1729–1737.

89. Skwark, M.J., Raimondi, D., Michel, M., and Elofsson, A. (2014). Improved contact predictions using the recognition of protein like contact patterns. PLoS Comput. Biol. 10, e1003889.

90. Monastyrskyy, B., D’Andrea, D., Fidelis, K., Tramontano, A., and Kryshtafovych, A. (2015). New encouraging developments in contact prediction: Assessment of the CASP11 results. Proteins., doi: 10.1002/prot.24943.

91. Jaynes, E.T. (1957). Information Theory and Statistical Mechanics I. Phys. Rev. 106, 620–630., doi: 10.1103/PhysRev.106.620.

92. Jaynes, E.T. (1957). Information Theory and Statistical Mechanics. II. Phys. Rev. 108, 171–190., doi: 10.1103/PhysRev.108.171.

93. Wainwright, M.J., and Jordan, M.I. (2007). Graphical Models, Exponential Families, and Variational Inference. Found. Trends Mach. Learn. 1, 1–305., doi: 10.1561/2200000001.

94. Murphy, K.P. (2012). Machine Learning: A Probabilistic Perspective (MIT Press).

95. Morcos, F., Pagnani, A., Lunt, B., Bertolino, A., Marks, D.S., Sander, C., Zecchina, R., Onuchic, J.N., Hwa, T., and Weigt, M. (2011). Direct-coupling analysis of residue coevolution captures native contacts across many protein families. Proc. Natl. Acad. Sci. U. S. A. 108, E1293–301., doi: 10.1073/pnas.1111471108.

39. Marks, D.S., Colwell, L.J., Sheridan, R., Hopf, T.A., Pagnani, A., Zecchina, R., and Sander, C. (2011). Protein 3D structure computed from evolutionary sequence variation. PLoS One 6, e28766., doi: 10.1371/journal.pone.0028766.

96. Cocco, S., Feinauer, C., Figliuzzi, M., Monasson, R., and Weigt, M. (2017). Inverse Statistical Physics of Protein Sequences: A Key Issues Review. arXiv.

97. Koller, D., and Friedman, N.I.R. (2009). Probabilistic graphical models: Principles and Techniques (MIT Press).

99. Stein, R.R., Marks, D.S., and Sander, C. (2015). Inferring Pairwise Interactions from Biological Data Using Maximum-Entropy Probability Models. PLOS Comput. Biol. 11, e1004182.

100. Seemayer, S., Gruber, M., and Söding, J. (2014). CCMpred-fast and precise prediction of protein residue-residue contacts from correlated mutations. Bioinformatics, btu500.

102. Kamisetty, H., Ovchinnikov, S., and Baker, D. (2013). Assessing the utility of coevolution-based residue-residue contact predictions in a sequence- and structure-rich era. Proc. Natl. Acad. Sci. U. S. A. 110, 15674–9., doi: 10.1073/pnas.1314045110.

103. Lapedes, A., Giraud, B., and Jarzynski, C. (2012). Using Sequence Alignments to Predict Protein Structure and Stability With High Accuracy.

104. Balakrishnan, S., Kamisetty, H., Carbonell, J.G., Lee, S.-I., and Langmead, C.J. (2011). Learning generative models for protein fold families. Proteins 79, 1061–78., doi: 10.1002/prot.22934.

98. Ekeberg, M., Lövkvist, C., Lan, Y., Weigt, M., and Aurell, E. (2013). Improved contact prediction in proteins: Using pseudolikelihoods to infer Potts models. Phys. Rev. E 87, 012707., doi: 10.1103/PhysRevE.87.012707.

105. Friedman, J., Hastie, T., and Tibshirani, R. (2008). Sparse inverse covariance estimation with the graphical lasso. Biostatistics 9, 432–41., doi: 10.1093/biostatistics/kxm045.

106. Banerjee, O., El Ghaoui, L., and D’Aspremont, A. (2008). Model Selection Through Sparse Maximum Likelihood Estimation for Multivariate Gaussian or Binary Data. J. Mach. Learn. Res. 9, 485–516.

107. Baldassi, C., Zamparo, M., Feinauer, C., Procaccini, A., Zecchina, R., Weigt, M., and Pagnani, A. (2014). Fast and accurate multivariate gaussian modeling of protein families: predicting residue contacts and protein-interaction partners. PLoS One 9, e92721., doi: 10.1371/journal.pone.0092721.

101. Ekeberg, M., Hartonen, T., and Aurell, E. (2014). Fast pseudolikelihood maximization for direct-coupling analysis of protein structure from many homologous amino-acid sequences. J. Comput. Phys. 276, 341–356.

108. Besag, J. (1975). Statistical Analysis of Non-Lattice Data. Source Stat. 24, 179–195.

109. Gidas, B. (1988). Consistency of maximum likelihood and pseudo-likelihood estimators for Gibbs Distributions. Stoch. Differ. Syst. Stoch. Control Theory Appl.

110. Feinauer, C., Skwark, M.J., Pagnani, A., and Aurell, E. (2014). Improving contact prediction along three dimensions. 19.

111. Zhang, H., Huang, Q., Bei, Z., Wei, Y., and Floudas, C.A. (2016). COMSAT: Residue contact prediction of transmembrane proteins based on support vector machines and mixed integer linear programming. Proteins Struct. Funct. Bioinforma., n/a–n/a., doi: 10.1002/prot.24979.