1.3 Applications

The most popular and historically motivated application for contact prediction is contact-guided de novo structure prediction.

It has long been known that the native protein 3D structure can be reconstructed from an error-free contact map [43]. Also, protein fold reconstruction from sparse inter-residue proximity constraints obtained from experiments such as cross-linking/mass spectrometry, Foerster resonance energy transfer (FRET) or sparse nuclear Overhauser enhancement (NOE) distance data generated from NMR experiments has been demonstrated [35,112–116]. Predicted contacts, however, have long been regarded as being of little use for structure prediction because of their high false-positive rates [117,118]. Only with the emergence of global statistical models for contact prediction which drastically reduced false-positive rates there has been renewed interest in de novo structure prediction aided by predicted contacts. In 2011, Marks et al. showed that the top scoring contacts predicted with their mean-field approach mfDCA are sufficiently accurate to successfully deduce the native fold of the protein [39]. In the following years, methods to predict contacts have been improved and applied to model many more protein structures culminating in the high-throughput prediction of 614 protein structures out of which more than 100 represent novel folds by Ovchinnikov and colleagues in 2017 [119–127].

Many contact-guided protocols have been established since, that typically integrate predicted contacts in form of distance constraints into an energy function to guide the conformational sampling process: Unicon3D [128], RASREC [129], RBOAleph [130], GDFuzz3D [131], PconsFold [132], C2S_Pipeline [133], FRAGFOLD + PSICOV [134], FILM3 [135], EVFold [39]. Figure 1.6 presents a generalized structure prediction pipeline using predicted contacts.

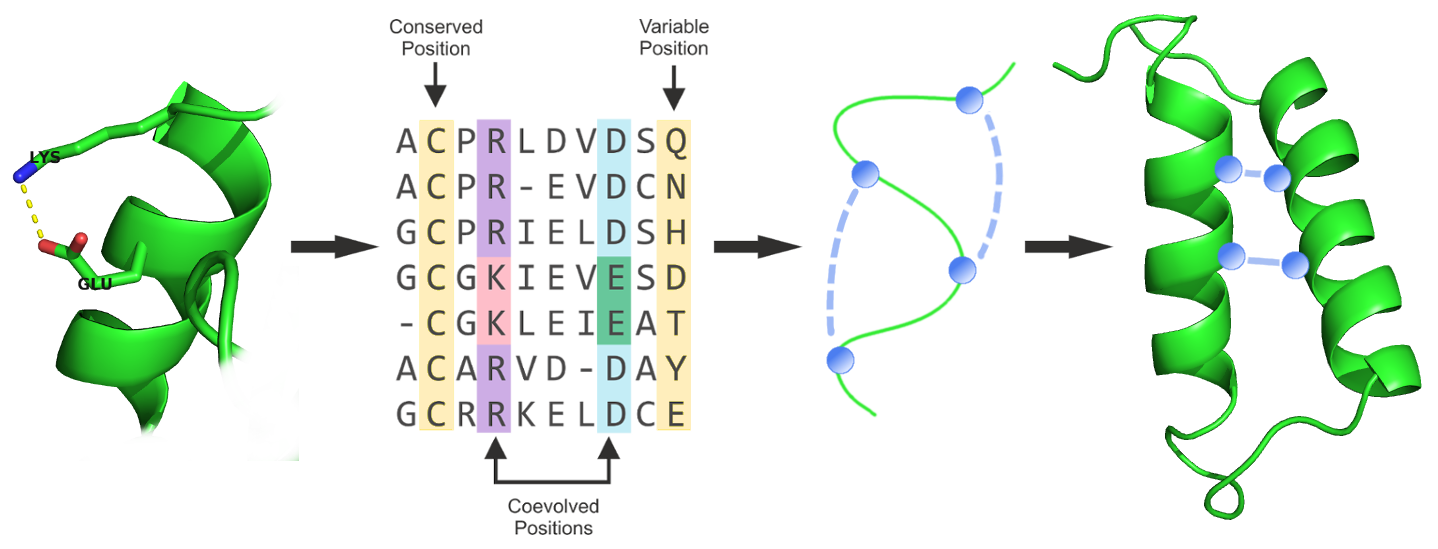
Figure 1.6: Generalized structure prediction pipeline integrating predicted contacts in form of distance constraints that guide conformational sampling.

The optimal quality of inferred contacts and their effective utilization is still subject to discussion and further research. It has been demonstrated that only a small subset of native contacts is sufficient to produce accurate structural models [43,44,133,136–138]. Sathyapriya and colleagues developed a rational strategy to select important native contacts and successfully reconstructed the structure to near native resolution with only 8% of contacts [136]. Kim and colleagues formulated that only one correct contact for every 12 residues in the protein is sufficient to allow accurate topology level modeling given that the contacts are nonlocal and broadly distributed [44]. These studies emphasize that certain contacts are more important than others. Long-range contacts are rare and most informative for protein structure prediction because they define the overal fold and packing of tertiary structure whereas short-range contacts define local secondary structure [139]. It is a consistent finding that eventhough long-range contacts are of higher relevance than short-range contacts for structure reconstruction, their information alone is not sufficient [134,136,140]. Since a small number of correct residue-residue contacts is sufficient to improve protein structure prediction and many reconstruction protocols can tolerate missing contact information much better than erroneous contact information, it has been stressed that methods development should focus on predicting a small number of high confident contacts [44,45]. Marks and colleagues observed that isolated false positives have a much stronger detrimental effect on structure prediction than false positives close to true contacts [39]. Zhang et al. found that their tool Touchstone II required an accuracy of long-range contact predictions of at least 22% to generate a positive effect to structure prediction [141]. Frequently, folding protocols employ a filtering step to eliminate unsatisfied or conflicting constraints possibly originating from false-positive contacts [142,143]. Generally it is assumed that higher precision of predicted long-range contacts results in improved structural models, albeit there is no strong correlation as model quality depends on many other factors such as the secondary structure composition of the protein, the domain size, the usage of additional sources of structural information, the type of distance constraint function and the particular structure reconstruction protocol [39,134,139,141,144].

Coevolution has not only been studied for residues pairs within a protein but also for residue pairs across protein–protein interfaces [120,121,126,145,146]. Eventhough the methodology of detecting coevolving amino acid pairs from the MSA is the same, a new challenge arises for the correct identification of orthologous interacting partners. Without the correct pairing of interacting partners for every species the detection of coevolutionary signals would be compromised. However, the generation of a MSA of paired sequences is complicated in the presence of multiple paralogs of a gene in a single genome. The problem of paralog matching is visualized in Figure 1.7. For prokaryotes, sequence paires are typically identified by exploiting the bacterial gene organisation in form of operons, i.e. co-localized genes will be co-expressed and are more likely to physically interact. Co-localisation of genes has also been applied to match genes from eurkaryotes, assuming that Uniprot accession numbers can be used as a proxy for genomic distances [146]. New strategies have been developed based on the idea that an alignment with correctly matched paralogs will maximize the coevolution score [147,148].

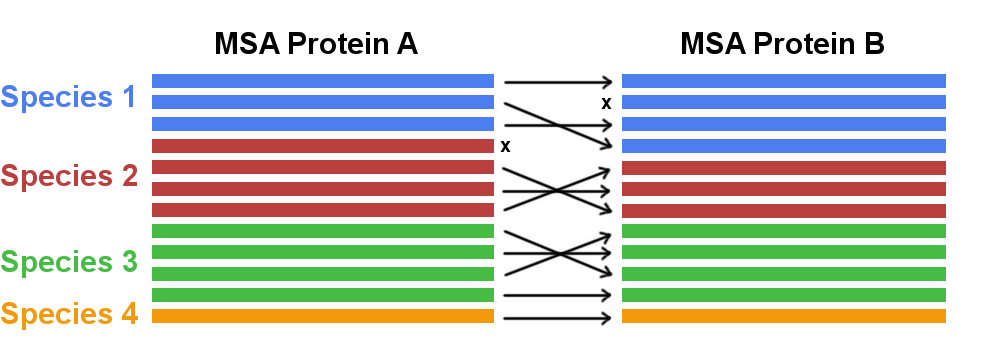
Figure 1.7: Concatenating two multiple sequence alignments. In case multiple paralogs exist for a gene in one species the correct interaction partner needs to be identified and matched (marked with arrows). Sequences that cannot be paired with a unique interaction partner need to be discarded (marked with x).

A related objective is the study of the oligomerization status of proteins. The study of homo-oligomers is simplified in the sense that the identical protein sequence of both interaction partners renders the concatenation of two MSAs unnessary and allows to work with one MSA. A different challenge lies in the correct distinction between the physical contacts of the monomeric structure and the interprotein contacts. With the availability of monomeric structural data the idea is to filter out those high scoring contacts that form contacts in the monomeric structure or are located in the protein core. The remaining high scoring false positive contacts at the surface of the protein are potential contacts at the interface that can be incorporated into a docking protocol to drive complex formation [149,150].

Predicted contacts have also been appplied in the analysis of potential alternative conformations of proteins [41,151–155]. Coevolutionary analysis detects all evolutionarily significant residue–residue correlations, regardless of whether the interaction is formed in a transient state of the protein or its stable form. Therefore, predicted contact maps might capture multiple states of a protein, since they are of functional importance and thus under evolutionary pressure. Sfriso and colleagues developed an automated pipiline that introduces filtered predicted contacts as ensemble restraints into a molecular dynamics simulations and is able to detect alternative relevant conformational states [151].

Eventhough the coevolutionary methods have been developed for proteins, they have been successfully applied to analyse nucleotide coevolution and to predict RNA tertiary structures with the help of predicted nucleotide-nucleotide contacts [156–158]. Much less RNA sequences are required compared to protein sequences in order to extract statistically significant signals because of the reduced number of model parameters when working with a four letter alphabet (compared to a 20 letter alphabet with proteins). On the downside, alignment errors resulting from the complicated determination of RNA multiple sequence alignments limits the accuracy of coevolution analysis [158]. Despite the diminished accuracy, predicted nucleotide contacts have been demonstrated to improve RNA structure prediction over conventional methods [157].

Predicted residue-residue contacts have been used to tackle various other problems in the area of structural biology. Sadowski used predicted contacts to parse domain boundaries based on the simple idea that contacts are more abundant within domains than between domains [40]. Contact maps display patterns that reflect secondary structure elements, which can be parsed to detect alpha helices and beta-sheets [88,159]. Quality assessment of structural models, involving model selection and ranking, is a crucial task in structural biology. Predicted residue-residue contacts can indicate the best protein structure among a set of properly folded and misfolded structures by counting the number of satisfied contacts [118,160]. Besides ranking of models, predicted contacts have been used as features for training machine learning methods that predict the global quality of a structural model [161,162].

The mathematical framework of the coevolution models used to predict residue-residue proteins has been found to be useful in other fields of biology beyond structure prediction. Skwark and colleagues applied the popular coevolution statistical models to genomes and developed a statistical method called genomeDCA [163,164]. They are able to identify coevolving polymorphic locus pairs based on the idea that the corresponding proteins form protein-protein interactions that are under strong evolutionary pressure. In a case study on two large human pathogen populations they found that three quarters of coevolving loci are located in genes that determine beta-lactam (antibiotic) resistence.

The stastistical models used for coevolution analysis provide information about which residue pairs are important in evolution for folding or functional constraints. They can be used to assign probabilities to sequences that reflect the overal compliance of a sequence with the protein family under study and thereby provide quantitative predictions of mutational effects [42,165,166]. Computational screening of mutational effects can support and complement the costly and time-consuming directed evolution or mutational screening experiments [42]. With a similar idea in mind, the coevolution models have been applied to sequences of human immune repertoires [167,168]. Antibody affinity maturation can be viewed as a Darwinian process with the affinity to the target antigen being the main fitness criterion. Therefore, given the model representing the antibody sequence family, the probability for a sequence reflects the binding affinity to the target antigen. Quantifying the effect of mutations is also helpful for protein design. Coevolving positions might be of particular interest as hotspots for engineering protein stability or functional specificity because they determine positions relevant to protein structure and function [169]. The interpretation of the model parameters as energies has hlped to analyse the sequence capacity of protein folds, that is how many sequences can fold into a specific structure [170].

Fox and colleagues turn the idea of DCA upside down. They developed a benchmark for testing the accuracy of large MSAs by evaluating the agreeement between the predicted and the native contacts [171]. Based on the assumption that better alignments provide more accurate contact predictions, the alignment quality is inferred from the precision of predicted contacts.

References

43. Vendruscolo, M., Kussell, E., and Domany, E. (1997). Recovery of protein structure from contact maps. Fold. Des. 2, 295–306., doi: 10.1016/S1359-0278(97)00041-2.

35. Li, W., Zhang, Y., and Skolnick, J. (2004). Application of sparse NMR restraints to large-scale protein structure prediction. Biophys. J. 87, 1241–8., doi: 10.1529/biophysj.104.044750.

112. Yu, X., Wu, X., Bermejo, G.A., Brooks, B.R., and Taraska, J.W. (2013). Accurate high-throughput structure mapping and prediction with transition metal ion FRET. Structure 21, 9–19., doi: 10.1016/j.str.2012.11.013.

116. Aszódi, A., Taylor, W.R., and Gradwell, M.J. (1995). Global Fold Determination from a Small Number of Distance Restraints. J. Mol. Biol. 251, 308–326., doi: 10.1006/JMBI.1995.0436.

117. Wu, S., Szilagyi, A., and Zhang, Y. (2011). Improving protein structure prediction using multiple sequence-based contact predictions. Structure 19, 1182–1191., doi: 10.1016/j.str.2011.05.004.

118. Tress, M.L., and Valencia, A. (2010). Predicted residue-residue contacts can help the scoring of 3D models. Proteins Struct. Funct. Bioinforma. 78, NA—–NA., doi: 10.1002/prot.22714.

39. Marks, D.S., Colwell, L.J., Sheridan, R., Hopf, T.A., Pagnani, A., Zecchina, R., and Sander, C. (2011). Protein 3D structure computed from evolutionary sequence variation. PLoS One 6, e28766., doi: 10.1371/journal.pone.0028766.

119. Hopf, T.A., Colwell, L.J., Sheridan, R., Rost, B., Sander, C., and Marks, D.S. (2012). Three-dimensional structures of membrane proteins from genomic sequencing. Cell 149, 1607–21., doi: 10.1016/j.cell.2012.04.012.

127. Ovchinnikov, S., Park, H., Varghese, N., Huang, P.-S., Pavlopoulos, G.A., Kim, D.E., Kamisetty, H., Kyrpides, N.C., and Baker, D. (2017). Protein structure determination using metagenome sequence data. Science (80-. ). 355, 294–298., doi: 10.1126/science.aah4043.

128. Bhattacharya, D., Cao, R., and Cheng, J. (2016). UniCon3D: de novo protein structure prediction using united-residue conformational search via stepwise, probabilistic sampling. Bioinformatics, btw316., doi: 10.1093/bioinformatics/btw316.

129. Braun, T., Koehler Leman, J., and Lange, O.F. (2015). Combining Evolutionary Information and an Iterative Sampling Strategy for Accurate Protein Structure Prediction. PLoS Comput. Biol. 11, e1004661., doi: 10.1371/journal.pcbi.1004661.

130. Mabrouk, M., Putz, I., Werner, T., Schneider, M., Neeb, M., Bartels, P., and Brock, O. (2015). RBO Aleph: leveraging novel information sources for protein structure prediction. Nucleic Acids Res. 43, W343–8.

131. Pietal, M.J., Bujnicki, J.M., and Kozlowski, L.P. (2015). GDFuzz3D: a method for protein 3D structure reconstruction from contact maps, based on a non-Euclidean distance function. Bioinformatics, btv390.

132. Michel, M., Hayat, S., Skwark, M.J., Sander, C., Marks, D.S., and Elofsson, A. (2014). PconsFold: improved contact predictions improve protein models. Bioinformatics 30, i482–i488.

133. Konopka, B.M., Ciombor, M., Kurczynska, M., and Kotulska, M. (2014). Automated Procedure for Contact-Map-Based Protein Structure Reconstruction. J. Membr. Biol., doi: 10.1007/s00232-014-9648-x.

134. Kosciolek, T., and Jones, D.T. (2014). De novo structure prediction of globular proteins aided by sequence variation-derived contacts. PLoS One 9, e92197.

135. Nugent, T., and Jones, D.T. (2012). Accurate de novo structure prediction of large transmembrane protein domains using fragment-assembly and correlated mutation analysis. Proc. Natl. Acad. Sci. U. S. A. 109, E1540–7., doi: 10.1073/pnas.1120036109.

44. Kim, D.E., Dimaio, F., Yu-Ruei Wang, R., Song, Y., and Baker, D. (2014). One contact for every twelve residues allows robust and accurate topology-level protein structure modeling. Proteins 82 Suppl 2, 208–18.

136. Sathyapriya, R., Duarte, J.M., Stehr, H., Filippis, I., and Lappe, M. (2009). Defining an essence of structure determining residue contacts in proteins. PLoS Comput. Biol. 5, e1000584., doi: 10.1371/journal.pcbi.1000584.

138. Vassura, M., Margara, L., Di Lena, P., Medri, F., Fariselli, P., and Casadio, R. (2007). Reconstruction of 3D structures from protein contact maps. IEEE/ACM Trans. Comput. Biol. Bioinform. 5, 357–67., doi: 10.1109/TCBB.2008.27.

139. Adhikari, B., Bhattacharya, D., Cao, R., and Cheng, J. (2017). Assessing Predicted Contacts for Building Protein Three-Dimensional Models. Methods Mol. Biol. 1484, 115–126., doi: 10.1007/978-1-4939-6406-2_9.

140. Di Lena, P., Vassura, M., Margara, L., Fariselli, P., and Casadio, R. (2009). On the Reconstruction of Three-dimensional Protein Structures from Contact Maps. Algorithms 2, 76–92., doi: 10.3390/a2010076.

45. Duarte, J.M., Sathyapriya, R., Stehr, H., Filippis, I., and Lappe, M. (2010). Optimal contact definition for reconstruction of contact maps. BMC Bioinformatics 11., doi: 10.1186/1471-2105-11-283.

141. Zhang, Y., Kolinski, A., and Skolnick, J. (2003). TOUCHSTONE II: a new approach to ab initio protein structure prediction. Biophys. J. 85, 1145–64., doi: 10.1016/S0006-3495(03)74551-2.

142. Wang, S., Li, W., Zhang, R., Liu, S., and Xu, J. (2016). CoinFold: a web server for protein contact prediction and contact-assisted protein folding. Nucleic Acids Res., gkw307., doi: 10.1093/nar/gkw307.

143. Adhikari, B., Bhattacharya, D., Cao, R., and Cheng, J. (2015). CONFOLD: Residue-residue contact-guided ab initio protein folding. Proteins 83, 1436–49.

144. Oliveira, S.H.P. de, Shi, J., and Deane, C.M. (2016). Comparing co-evolution methods and their application to template-free protein structure prediction. Bioinformatics, btw618., doi: 10.1093/bioinformatics/btw618.

120. Ovchinnikov, S., Kamisetty, H., and Baker, D. (2014). Robust and accurate prediction of residue-residue interactions across protein interfaces using evolutionary information. Elife 3, e02030.

121. Hopf, T.A., Schärfe, C.P.I., Rodrigues, J.P.G.L.M., Green, A.G., Sander, C., Bonvin, A.M.J.J., and Marks, D.S. (2014). Sequence co-evolution gives 3D contacts and structures of protein complexes.

126. Ovchinnikov, S., Kinch, L., Park, H., Liao, Y., Pei, J., Kim, D.E., Kamisetty, H., Grishin, N.V., and Baker, D. (2015). Large scale determination of previously unsolved protein structures using evolutionary information. Elife 4, e09248.

145. Rodriguez-Rivas, J., Marsili, S., Juan, D., and Valencia, A. (2016). Conservation of coevolving protein interfaces bridges prokaryote-eukaryote homologies in the twilight zone. Proc. Natl. Acad. Sci. U. S. A. 113, 15018–15023., doi: 10.1073/pnas.1611861114.

146. Feinauer, C., Szurmant, H., Weigt, M., and Pagnani, A. (2016). Inter-Protein Sequence Co-Evolution Predicts Known Physical Interactions in Bacterial Ribosomes and the Trp Operon. PLoS One 11, e0149166., doi: 10.1371/journal.pone.0149166.

147. Gueudré, T., Baldassi, C., Zamparo, M., Weigt, M., and Pagnani, A. (2016). Simultaneous identification of specifically interacting paralogs and inter-protein contacts by Direct-Coupling Analysis. 19.

148. Bitbol, A.-F., Dwyer, R.S., Colwell, L.J., and Wingreen, N.S. (2016). Inferring interaction partners from protein sequences. Proc. Natl. Acad. Sci. 113, 12180–12185., doi: 10.1073/pnas.1606762113.

149. Uguzzoni, G., John Lovis, S., Oteri, F., Schug, A., Szurmant, H., and Weigt, M. (2017). Large-scale identification of coevolution signals across homo-oligomeric protein interfaces by direct coupling analysis. Proc. Natl. Acad. Sci. 114, E2662—–E2671., doi: 10.1073/pnas.1615068114.

150. Dos Santos, R.N., Morcos, F., Jana, B., Andricopulo, A.D., and Onuchic, J.N. (2015). Dimeric interactions and complex formation using direct coevolutionary couplings. Sci. Rep. 5, 13652.

41. Parisi, G., Zea, D.J., Monzon, A.M., and Marino-Buslje, C. (2015). Conformational diversity and the emergence of sequence signatures during evolution. Curr. Opin. Struct. Biol. 32C, 58–65.

151. Sfriso, P., Duran-Frigola, M., Mosca, R., Emperador, A., Aloy, P., and Orozco, M. (2016). Residues Coevolution Guides the Systematic Identification of Alternative Functional Conformations in Proteins. Structure 24, 116–126., doi: 10.1016/j.str.2015.10.025.

155. Jeon, J., Nam, H.-J., Choi, Y.S., Yang, J.-S., Hwang, J., and Kim, S. (2011). Molecular evolution of protein conformational changes revealed by a network of evolutionarily coupled residues. Mol. Biol. Evol. 28, 2675–85.

156. Nawy, T. (2016). Structural biology: RNA structure from sequence. Nat. Methods 13, 465–465., doi: 10.1038/nmeth.3892.

158. De Leonardis, E., Lutz, B., Ratz, S., Cocco, S., Monasson, R., Schug, A., and Weigt, M. (2015). Direct-Coupling Analysis of nucleotide coevolution facilitates RNA secondary and tertiary structure prediction. Nucleic Acids Res., gkv932.

157. Weinreb, C., Gross, T., Sander, C., and Marks, D.S. (2015). 3D RNA from evolutionary couplings.

40. Sadowski, M.I. (2013). Prediction of protein domain boundaries from inverse covariances. Proteins 81, 253–260., doi: 10.1002/prot.24181.

88. Andreani, J., and Söding, J. (2015). Bbcontacts: Prediction of $$-strand pairing from direct coupling patterns. Bioinformatics 31, 1729–1737.

159. Suvarna Vani, K., and Praveen Kumar, K. (2018). Feature Extraction of Protein Contact Maps from Protein 3D-Coordinates. In Inf. commun. technol. adv. intell. syst. comput. (Springer, Singapore), pp. 311–320., doi: 10.1007/978-981-10-5508-9_30.

160. Woźniak Pawełand Kotulska, M., and Vriend, G. (2017). Correlated mutations distinguish misfolded and properly folded proteins. Bioinformatics 33, 1497–1504., doi: 10.1093/bioinformatics/btx013.

161. Cao, R., Adhikari, B., Bhattacharya, D., Sun, M., Hou, J., and Cheng, J. (2016). QAcon: single model quality assessment using protein structural and contact information with machine learning techniques. Bioinformatics 14, btw694., doi: 10.1093/bioinformatics/btw694.

162. Terashi, G., Nakamura, Y., Shimoyama, H., and Takeda-Shitaka, M. (2014). Quality Assessment Methods for 3D Protein Structure Models Based on a Residue–Residue Distance Matrix Prediction. Chem. Pharm. Bull. 62, 744–753.

163. Skwark, M.J., Croucher, N.J., Puranen, S., Chewapreecha, C., Pesonen, M., Xu, Y.Y., Turner, P., Harris, S.R., Beres, S.B., and Musser, J.M. et al. (2017). Interacting networks of resistance, virulence and core machinery genes identified by genome-wide epistasis analysis. PLOS Genet. 13, e1006508., doi: 10.1371/journal.pgen.1006508.

164. Gao, C.-Y., Zhou, H.-J., and Aurell, E. (2017). Correlation-Compressed Direct Coupling Analysis. arXiv.

42. Hopf, T.A., Ingraham, J.B., Poelwijk, F.J., Schärfe, C.P.I., Springer, M., Sander, C., and Marks, D.S. (2017). Mutation effects predicted from sequence co-variation. Nat. Biotechnol. 35, 128–135., doi: 10.1038/nbt.3769.

165. Wu, N.C., Du, Y., Le, S., Young, A.P., Zhang, T.-H., Wang, Y., Zhou, J., Yoshizawa, J.M., Dong, L., and Li, X. et al. (2016). Coupling high-throughput genetics with phylogenetic information reveals an epistatic interaction on the influenza A virus M segment. BMC Genomics 17, 46., doi: 10.1186/s12864-015-2358-7.

166. Figliuzzi, M., Jacquier, H., Schug, A., Tenaillon, O., and Weigt, M. (2015). Coevolutionary landscape inference and the context-dependence of mutations in beta-lactamase TEM-1. Mol. Biol. Evol., msv211., doi: 10.1093/molbev/msv211.

167. Asti, L., Uguzzoni, G., Marcatili, P., and Pagnani, A. (2016). Maximum-Entropy Models of Sequenced Immune Repertoires Predict Antigen-Antibody Affinity. PLoS Comput. Biol. 12, e1004870.

168. Elhanati, Y., Murugan, A., Callan, C.G., Mora, T., and Walczak, A.M. (2014). Quantifying selection in immune receptor repertoires. Proc. Natl. Acad. Sci. U. S. A. 111, 9875–9880., doi: 10.1073/pnas.1409572111.

169. Franceus, J., Verhaeghe, T., and Desmet, T. (2016). Correlated positions in protein evolution and engineering. J. Ind. Microbiol. Biotechnol., 1–9., doi: 10.1007/s10295-016-1811-1.

170. Tian, P., and Best, R.B. (2017). How Many Protein Sequences Fold to a Given Structure? A Coevolutionary Analysis. Biophys. J. 113, 1719–1730., doi: 10.1016/j.bpj.2017.08.039.

171. Fox, G., Sievers, F., and Higgins, D.G. (2016). Using de novo protein structure predictions to measure the quality of very large multiple sequence alignments. Bioinformatics 32, 814–20., doi: 10.1093/bioinformatics/btv592.