5.7 Methods

5.7.1 Modelling the Prior Over Couplings Depending on Contact States

The mixture weights \(g_k(\cij)\) in eq. (5.4) are modelled as softmax:

\[\begin{equation} g_k(\cij) = \frac{\exp \gamma_k(\cij)}{\sum_{k'=0}^K \exp \gamma_{k'}(\cij)} \tag{5.6} \end{equation}\]

The functions \(g_k(\cij)\) remain invariant when adding an offset to all \(\gamma_k(\cij)\). This degeneracy can be removed by setting \(\gamma_0(\cij)=1\).

5.7.2 Gaussian Approximation to the Posterior of Couplings

From sampling experiments done by Markus Gruber we know that the regularized pseudo-log-likelihood for realistic examples of protein MSAs obeys the equipartition theorem. The equipartition theorem states that in a harmonic potential (where third and higher order derivatives around the energy minimum vanish) the mean potential energy per degree of freedom (i.e. per eigendirection of the Hessian of the potential) is equal to \(k_B T/2\), which is of course equal to the mean kinetic energy per degree of freedom. Hence we have a strong indication that in realistic examples the pseudo log likelihood is well approximated by a harmonic potential. We assume here that this will also be true for the regularized log likelihood.

The posterior distribution of couplings \(\w\) is given by

\[\begin{equation} p(\w | \X , \v^*) = p(\X | \v^*, \w) \Gauss (\w | \mathbf{0}, \lambda_w^{-1} \I) \end{equation}\]

where the single potentials \(\v\) are set to the target vector \(\v^*\) as discussed in section 5.1.

The posterior distribution can be approximated with a so called “Laplace Approximation”[94]: by performing a second order Taylor expansion around the mode \(\w^*\) of the log posterior it can be written as

\[\begin{align} \log p(\w | \X , \v^*) \overset{!}{\approx} & \; \log p(\w^* | \X , \v^*) \nonumber\\ & + \nabla_\w \log p(\w | \X , \v^*)|_{\w^*}(\w-\w^*) \nonumber\\ & - \frac{1}{2} (\w-\w^*)^{\mathrm{T}} \H (\w-\w^*) \; . \end{align}\]

where \(\H\) signifies the negative Hessian matrix with respect to the components of \(\w\),

\[\begin{equation} (\H)_{klcd, ijab} = - \left. \frac{\partial^2 \log p(\w | \X , \v^{*})}{\partial \w_{klcd} \, \partial \wijab } \right|_{(\w^{*})} \; . \end{equation}\]

The mode \(\w^*\) will be determined with the CD approach described in detail in section 3. Since the gradient vanishes at the mode maximum, \(\nabla_\w \log p(\w | \X , \v^*)|_{\w^*} = 0\), the second order approximation can be written as

\[\begin{equation} \log p(\w | \X , \v^*) {\approx} \log p(\w^* | \X , \v^*) - \frac{1}{2} (\w-\w^*)^{\mathrm{T}} \, \H \, (\w-\w^*) \;. \end{equation}\]

Hence, the posterior of couplings can be approximated with a Gaussian

\[\begin{align} p(\w | \X , \v^*) &\approx p(\w^* | \X , \v^*) \exp \left( - \frac{1}{2} (\w-\w^*)^{\mathrm{T}} \H (\w -\w^*) \right) \nonumber \\ &= p(\w^* | \X , \v^*) \frac{(2 \pi)^\frac{D}{2}} { |\H|^\frac{D}{2}} \times \Gauss (\w | \w^*, \H^{-1} ) \nonumber \\ &\propto \Gauss (\w | \w^*, \H^{-1}) \,, \tag{5.7} \end{align}\]

with proportionality constant that depends only on the data and with a precision matrix equal to the negative Hessian matrix. The surprisingly easy computation of the Hessian can be found in Methods section 5.7.5.

5.7.3 Integrating out the Hidden Variables to Obtain the Likelihood Function of the Contact States

In order to compute the likelihood function of the contact states, one needs to solve the integral over \((\v, \w)\),

\[\begin{equation} p(\X | \c) = \int \int p(\X | \v,\w) \, p(\v, \w | \c) \,d\v\,d\w \; . \tag{5.8} \end{equation}\]

Inserting the prior over parameters \(p(\v, \w | \c)\) from eq. (5.3) into the previous equation and performing the integral over \(\v\), as discussed earlier in section 5.1, yields

\[\begin{eqnarray} p(\X | \c) &=& \int \left( \int p(\X | \v,\w) \, \Gauss(\v|\v^*,\lambda_v^{-1} \I) \,d\v \right) \, \prod_{1\le i<j\le L} p(\wij|\cij) \, d\w \\ p(\X | \c) &=& \int p(\X | \v^*,\w) \, \prod_{1\le i<j\le L} p(\wij|\cij) \, d\w \tag{5.9} \end{eqnarray}\]

Next, the likelihood of sequences, \(p(\X | \v^*,\w)\), will be multiplied with the regularisation prior \(\Gauss(\w|\mathbf{0}, \lambda_w^{-1} \I)\) and at the same time the coupling prior, which depends on the contact states, will be divided by the regularisation prior again:

\[\begin{eqnarray} p(\X | \c) &=& \int p(\X | \v^*,\w) \, \Gauss(\w|\mathbf{0}, \lambda_w^{-1} \I) \, \prod_{1\le i<j\le L} \frac{p(\wij|\cij)}{\Gauss(\wij|\mathbf{0}, \lambda_w^{-1} \I)} \,d\w \, . \end{eqnarray}\]

Now the crucial advantage of the likelihood regularisation is borne out: the strength of the regularisation prior, \(\lambda_w\), can be chosen such that the mode \(\w^*\) of the regularised likelihood is near to the mode of the integrand in the last integral. The regularisation prior \(\Gauss(\wij|\mathbf{0}, \lambda_w^{-1} \I)\) is then a simpler, approximate version of the real coupling prior \(\prod_{1\le i<j\le L} p(\wij|\cij)\) that depends on the contact state. This allows to approximate the regularised likelihood with a Gaussian distribution (eq. (5.7)), because this approximation will be fairly accurate in the region around its mode, which is near the region around the mode of the integrand and this again is in the region that contributes most to the integral:

\[\begin{eqnarray} p(\X | \c) &\propto& \int \Gauss (\w | \w^*, \H^{-1} ) \, \prod_{1 \le i<j \le L} \frac{p(\wij | \cij)}{\Gauss(\wij|\mathbf{0}, \lambda_w^{-1} \I)} d\w \,. \tag{5.10} \end{eqnarray}\]

The matrix \(\H\) has dimensions \((L^2 \times 20^2) \times (L^2 \times 20^2)\). Computing it is obviously infeasible, even if there was a way to compute \(p(x_i \eq a, x_j \eq b| \v^*,\w^*)\) efficiently. In Methods section 5.7.4 is shown that in practice, the off-diagonal block matrices with \((i,j) \ne (k,l)\) are negligible in comparison to the diagonal block matrices. For the purpose of computing the integral in eq. (5.10), it is therefore a good approximation to simply set the off-diagonal block matrices (case 3 in eq. (5.15)) to zero! The first term in the integrand of eq. (5.10) now factorizes over \((i,j)\),

\[\begin{equation} \Gauss (\w | \w^{*}, \H^{-1}) \approx \prod_{1 \le i < j \le L} \Gauss (\wij | \wij^{*}, \H_{ij}^{-1}) , \end{equation}\]

with the diagonal block matrices \((\H_{ij})_{ab,cd} := (\H)_{ijab,ijcd}\). Now the product over all residue indices can be moved in front of the integral and each integral can be performed over \(\wij\) separately,

\[\begin{eqnarray} p(\X | \c) &\propto& \int \prod_{1 \le i < j \le L} \Gauss (\wij | \wij^{*}, \H_{ij}^{-1}) \prod_{1 \le i<j \le L} \frac{p(\wij | \cij)}{\Gauss(\wij|\mathbf{0}, \lambda_w^{-1} \I)} d\w \\ p(\X | \c) &\propto& \int \prod_{1\le i<j\le L} \left( \Gauss (\wij | \wij^*, \H_{ij}^{-1}) \, \frac{p(\wij | \cij)}{\Gauss(\wij | \mathbf{0}, \lambda_w^{-1} \I)} \right) d\w \\ p(\X | \c) &\propto& \prod_{1\le i<j\le L} \int \Gauss (\wij | \wij^*, \H_{ij}^{-1}) \frac{p(\wij | \cij)}{\Gauss (\wij | \mathbf{0}, \lambda_w^{-1} \I)} d \wij \tag{5.11} \end{eqnarray}\]

Inserting the coupling prior defined in eq. (5.4) yields

\[\begin{eqnarray} p(\X | \c) &\propto& \prod_{1\le i<j\le L} \int \Gauss (\wij | \wij^*, \H_{ij}^{-1}) \frac{\sum_{k=0}^K g_{k}(\cij) \Gauss(\wij | \muk, \Lk^{-1})}{\Gauss (\wij | \mathbf{0}, \lambda_w^{-1} \I)} d \wij \\ p(\X | \c) &\propto& \prod_{1\le i<j\le L} \sum_{k=0}^K g_{k}(\cij) \int \frac{\Gauss (\wij | \wij^*, \H_{ij}^{-1})}{\Gauss (\wij | \mathbf{0}, \lambda_w^{-1} \I)} \Gauss(\wij | \muk, \Lk^{-1}) d\wij \; . \tag{5.12} \end{eqnarray}\] The integral can be carried out using the following formula: \[\begin{equation} \int d\seq \, \frac{ \Gauss( \seq | \mathbf{\mu}_1, \mathbf{\Lambda}_1^{-1}) }{\Gauss(\seq|\mathbf{0},\mathbf{\Lambda}3^{-1})} \, \Gauss(\seq|\mathbf{\mu}_2,\mathbf{\Lambda}_2^{-1}) = \\ \frac{\Gauss(\mathbf{0}| \mathbf{\mu}_1, \mathbf{\Lambda}_{1}^{-1}) \Gauss(\mathbf{0}| \mathbf{\mu}_2, \mathbf{\Lambda}_{2}^{-1})}{\Gauss(\mathbf{0}|\mathbf{0}, \mathbf{\Lambda}_{3}^{-1}) \Gauss(\mathbf{0}| \mathbf{\mu}_{12}, \mathbf{\Lambda}_{123}^{-1})} \end{equation}\] with \[\begin{eqnarray} \mathbf{\Lambda}_{123} &:=& \mathbf{\Lambda}_1 - \mathbf{\Lambda}_3 + \mathbf{\Lambda}_2 \\ \mathbf{\mu}_{12} &:=& \mathbf{\Lambda}_{123}^{-1}(\mathbf{\Lambda}_1 \mathbf{\mu}_1 + \mathbf{\Lambda}_2 \mathbf{\mu}_2). \end{eqnarray}\] We define \[\begin{align} \Lijk &:= \H_{ij} - \lambda_w \I + \Lk \\ \muijk &:= \Lijk^{-1}(\H_{ij} \wij^* + \Lk \muk) \,. \tag{5.13} \end{align}\]

and obtain

\[\begin{align} p(\X | \c) \propto \prod_{1 \le i < j \le L} \sum_{k=0}^K g_{k}(\cij) \frac{\Gauss( \mathbf{0} | \muk, \Lk^{-1})}{\Gauss(\mathbf{0} | \muijk, \Lijk^{-1})} \,. \tag{5.14} \end{align}\]

\(\Gauss( \mathbf{0} | \mathbf{0}, \lambda_w^{-1} \I)\) and \(\Gauss( \mathbf{0} | \wij^*, \H_{ij}^{-1})\) are constants that depend only on \(\X\) and \(\lambda_w\) and can be omitted.

5.7.4 The Hessian off-diagonal Elements Carry a Negligible Signal

Assume that \(\lambda_w=0\), i.e., no regularisation is applied. Suppose in columns \(i\) and \(j\) a set of sequences in the MSA contain amino acids \(a\) and \(b\) and the same sequences contain \(c\) and \(d\) in columns \(k\) and \(l\). Furthermore, assume that \((a,b)\) occur nowhere else in columns \(i\) and \(j\) and the same holds for \((c,d)\) in columns \(k\) and \(l\). This means that the coupling between \(a\) at position \(i\) and \(b\) at position \(j\) can be perfectly compensated by the coupling between \(c\) at position \(k\) and \(d\) at position \(l\). Adding \(10^6\) to \(w_{ijab}\) and substracting \(10^6\) from \(w_{klcd}\) leaves \(p(\X|\v,\w)\) unchanged. This means that \(w_{ijab}\) and \(w_{klcd}\) are almost perfectly negatively correlated in \(\Gauss(\w|\w^*,(\H)^{-1})\). Another way to see this is to evaluate \((\H)_{ijab,klcd}\) with eq. (5.15), which gives \((\H)_{klcd, ijab}=N_{ij}\,p(x_i \eq a, x_j \eq b| \v^*,\w^*) \, ( 1 - p(x_i \eq a, x_j \eq b| \v^*,\w^*)\) for this case. Under the assumption \(\lambda_w=0\), this precision matrix element is the same as the diagonal elements \((\H)_{ijab, ijab}\) and \((\H)_{klcd, klcd}\) (see case 2 in eq. (5.15)).

But when a realistic regularisation constant is assumed, e.g. \(\lambda_w \eq 0.2 L \approx 20\), \(w_{ijab}\) and \(w_{klcd}\) will be pushed to near zero, because the matrix element that couples \(w_{ijab}\) with \(w_{klcd}\), \(N_{ij}\,p(x_i \eq a, x_j \eq b| \v^*,\w^*) \, ( 1 - p(x_i \eq a, x_j \eq b| \v^*,\w^*)\) is the number of sequences that share amino acids \(a\) and \(b\) at position \((i,j)\) and \(c\) and \(d\) at position \((k,l)\), and this number is usually much smaller than \(\lambda_w\).

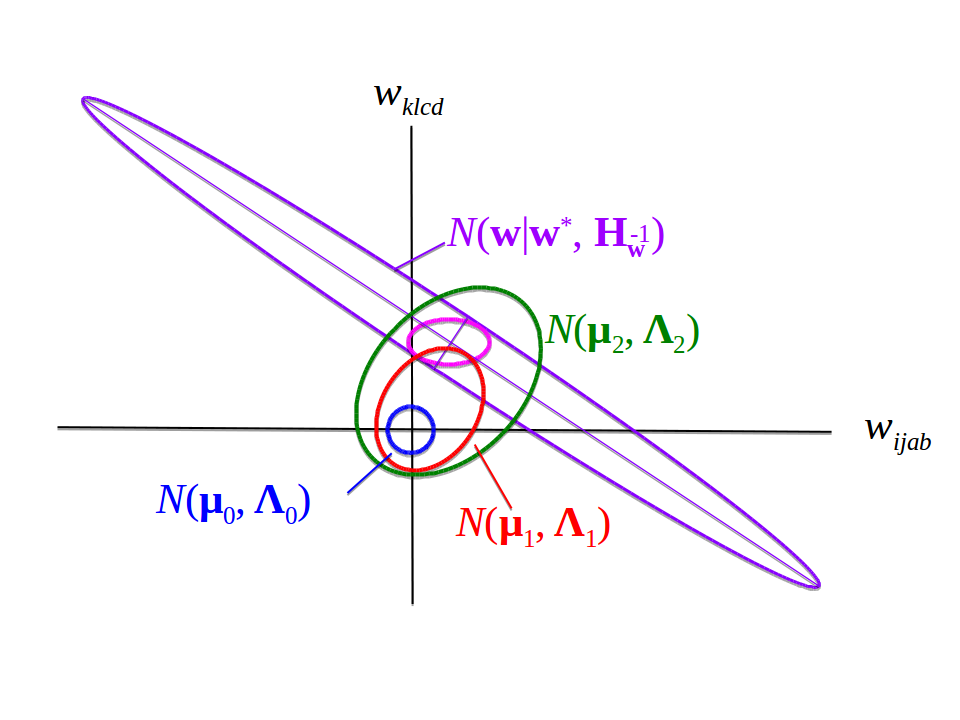
Figure 5.14: Setting the off-diagonal block matrices to zero in \(\H\) corresponds to replacing the violett Gaussian distrubution by the pink one. The ratios between the overlaps of \(\Gauss\!\left(\w \left| \w^*, \H^{-1} \right. \right)\) with the distributions \(\Gauss(\wij | \muk, \Lk^{-1})\) for various choices of \(k\) is only weakly affected by this replacement.

It is therefore a good approximation to set the off-diagonal block matrices \((\H)_{klcd, ijab}\) (case 3 in eq. (5.15)) to zero. This corresponds to replacing the violett distribution in Figure 5.14 by the pink one. To see why, first note that the functions \(g_k(\cij)\) and the component distributions \(\Gauss(\wij | \mu_k, \Lk^{-1})\) will be learned in such a way as to maximize the likelihood for predicting the correct contact state \(\c^m\) from the respective alignments \(\X^m\) for many MSAs of protein families \(m\). Therefore, these model parameters will adjust to the fact that the off-diagonal blocks in \(\H\) are neglected. Second, note that the integral over the product of \(\Gauss(\w | \w^*, \H^{-1})\) and \(\prod_{i<j} p(\wij | \cij) / \Gauss(\wij| 0, \lambda_w^{-1} \I)\) in eq. (5.10) evaluates the overlap of these two Gaussians. Third, the components of \(p(\wij|\cij)\) will be very much concentrated within a radius of less than \(1\) from the origin, because even residues with short \(C_\beta\)-\(C_\beta\) distance will rarely have coupling coefficients above \(1\). Fourth, the Gaussian components have no couplings between elements of \(\wij\) and \(\w_{kl}\), which is why they are axis-aligned (green in Figure 5.14). For these reasons, the relative strengths of the overlaps with different mixture components labeled by \(k\) in eq. (5.4) should be little affected by setting the off-diagonal block matrix couplings to zero.

5.7.5 Efficiently Computing the negative Hessian of the regularized log-likelihood

Surprisingly, the elements of the Hessian at the mode \(\w^*\) are easy to compute. Let \(i,j,k,l \in \{1,\ldots,L\}\) be columns in the MSA and let \(a, b, c, d \in \{1,\ldots,20\}\) represent amino acids. The partial derivative \(\partial / \partial \w_{klcd}\) of the second term in the gradient of the couplings in eq. (3.9) is

\[\begin{eqnarray} \frac{\partial^2 \LLreg(\v^*,\w)}{\partial \wklcd \, \partial \wijab } &=& - \sum_{n=1}^{N} \, \sum_{\mathbf{y} \in \Sn} \frac{\partial \left( \frac{\exp \left( \sum_{i=1}^L v_i(y_i) + \sum_{1 \le i < j \le L}^L w_{ij}(y_i,y_j) \right) }{Z_n(\v,\w)} \right)}{\partial \wklcd} I(y_i \eq a, y_j \eq b) \nonumber \\ &&- \lambda_w \delta_{ijab,klcd} \,, \end{eqnarray}\]

where \(\delta_{ijab,klcd} = I(ijab=klcd)\) is the Kronecker delta. Applying the product rule, it is found

\[\begin{eqnarray} \frac{\partial^2 \LLreg(\v^*,\w)}{\partial \wklcd \, \partial \wijab } &=& - \sum_{n=1}^{N} \, \sum_{\mathbf{y} \in \Sn} \frac{\exp \left(\sum_{i=1}^L v_i(y_i) + \sum_{1 \le i < j \le L}^L w_{ij}(y_i,y_j) \right)}{Z_n(\v,\w)} I(y_i \eq a, y_j \eq b) \nonumber \\ && \times \left[ \frac{\partial}{\partial \wklcd} \left( \sum_{i=1}^L v_i(y_i) + \sum_{1 \le i < j \le L} w_{ij}(y_i,y_j) \right) - \frac{1}{Z_n(\v,\w)} \frac{\partial Z_n(\v,\w) }{\partial\wklcd} \right] \nonumber\\ &&- \lambda_w \delta_{ijab,klcd} \\ \frac{\partial^2 \LLreg(\v^*,\w)}{\partial \wklcd \, \partial \wijab } &=& - \sum_{n=1}^{N} \, \sum_{\mathbf{y} \in \Sn} \frac{\exp \left(\sum_{i=1}^L v_i(y_i) + \sum_{1 \le i < j \le L}^L w_{ij}(y_i,y_j) \right)}{Z_n(\v,\w)} I(y_i \eq a, y_j \eq b) \nonumber\\ && \times \left[ I(y_k \eq c, y_l \eq d) - \frac{\partial}{\partial \wklcd} \log Z_n(\v,\w) \right] \nonumber\\ &&- \lambda_w \delta_{ijab,klcd} \,. \end{eqnarray}\]

This expression can be simpified using

\[\begin{equation} p(\mathbf{y} | \v,\w) = \frac{\exp \left( \sum_{i=1}^L v_i(y_i) + \sum_{1 \le i < j \le L} w_{ij}(y_i,y_j) \right)}{Z_n(\v,\w)} , \end{equation}\]

yielding

\[\begin{eqnarray} \frac{\partial^2 \LLreg(\v^*,\w)}{\partial \wklcd \, \partial \wijab} &=& - \sum_{n=1}^{N} \, \sum_{\mathbf{y} \in \Sn} p(\mathbf{y} | \v,\w) \, I(y_i \eq a, y_j \eq b, y_k \eq c, y_l \eq d) \nonumber \\ && + \sum_{n=1}^{N} \, \sum_{\mathbf{y} \in \mathcal{S}_n} p(\mathbf{y} | \v,\w) \, I(y_i \eq a, y_j \eq b ) \sum_{\mathbf{y} \in \Sn} p(\mathbf{y} | \v,\w) I(y_k \eq c, y_l \eq d ) \nonumber \\ && - \lambda_w \delta_{ijab,klcd} \,. \end{eqnarray}\]

If \(\X\) does not contain too many gaps, this expression can be approximated by

\[\begin{eqnarray} \frac{\partial^2 \LLreg(\v^*,\w)}{\partial \wklcd \, \partial \wijab } &=& - N_{ijkl} \: p(x_i \eq a, x_j \eq b, x_k \eq c, x_l \eq d | \v,\w) \nonumber \\ && + N_{ijkl} \: p(x_i \eq a, x_j \eq b | \v,\w) \, p(x_k \eq c, x_l \eq d | \v,\w) - \lambda_w \delta_{ijab,klcd} \,, \end{eqnarray}\]

where \(N_{ijkl}\) is the number of sequences that have a residue in \(i\), \(j\), \(k\) and \(l\).

Looking at three cases separately:

• case 1: \((k,l) = (i,j)\) and \((c,d) = (a,b)\)
• case 2: \((k,l) = (i,j)\) and \((c,d) \ne (a,b)\)
• case 3: \((k,l) \ne (i,j)\) and \((c,d) \ne (a,b)\),

the elements of \(\H\), which are the negative second partial derivatives of \(\LLreg(\v^*,\w)\) with respect to the components of \(\w\), are

\[\begin{eqnarray} \mathrm{case~1:} (\H)_{ijab, ijab} &=& N_{ij} \, p(x_i \eq a, x_j \eq b| \v^*,\w^*) \, ( 1 - p(x_i \eq a, x_j \eq b| \v^*,\w^*) \,) \nonumber \\ && +\lambda_w \\ \mathrm{case~2:} (\H)_{ijcd, ijab} &=& -N_{ij} \, p(x_i \eq a, x_j \eq b |\v^*,\w^*) \, p(x_i \eq c, x_j \eq d |\v^*,\w^*) \\ \mathrm{case~3:} (\H)_{klcd, ijab} &=& N_{ijkl} \, p(x_i \eq a, x_j \eq b, x_k \eq c, x_l \eq d | \v^*,\w^*) \nonumber \\ && -N_{ijkl} \, p(x_i \eq a, x_j \eq b | \v^*,\w^*)\, p(x_k \eq c, x_l \eq d | \v^*,\w^*) \,. \tag{5.15} \end{eqnarray}\]

We know from eq. (3.11) that at the mode \(\w^*\) the model probabilities match the empirical frequencies up to a small regularization term,

\[\begin{equation} p(x_i \eq a, x_j \eq b | \v^*,\w^*) = q(x_i \eq a, x_j \eq b) - \frac{\lambda_w}{N_{ij}} \wijab^* \,, \end{equation}\]

and therefore the negative Hessian elements in cases 1 and 2 can be expressed as

\[\begin{eqnarray} (\H)_{ijab, ijab} &=& N_{ij} \left( q(x_i \eq a, x_j \eq b) - \frac{\lambda_w}{N_{ij}} \wijab^* \right) \left( 1 - q(x_i \eq a, x_j \eq b) +\frac{\lambda_w}{N_{ij}} \wijab^* \right) \nonumber\\ && +\lambda_w \\ (\H)_{ijcd, ijab} &=& -N_{ij} \left(\,q(x_i \eq a, x_j \eq b) - \frac{\lambda_w}{N_{ij}} \wijab^* \right) \left( q(x_i \eq c, x_j \eq d) -\frac{\lambda_w}{N_{ij}} \wijcd^* \right) . \tag{5.16} \end{eqnarray}\]

In order to write the previous eq. (5.16) in matrix form, the regularised empirical frequencies \(\qij\) will be defined as

\[\begin{equation} (\qij)_{ab} = q'_{ijab} := q(x_i \eq a, x_j \eq b) - \lambda_w \wijab^* / N_{ij} \,, \end{equation}\]

and the \(400 \times 400\) diagonal matrix \(\Qij\) will be defined as

\[\begin{equation} \Qij := \text{diag}(\qij) \; . \end{equation}\]

Now eq. (5.16) can be written in matrix form

\[\begin{equation} \H_{ij} = N_{ij} \left( \Qij - \qij \qij^{\mathrm{T}} \right) + \lambda_w \I \; . \tag{5.17} \end{equation}\]

5.7.6 Efficiently Computing the Inverse of Matrix \(\Lijk\)

It is possible to efficiently invert the matrix \(\Lijk = \H_{ij} - \lambda_w \I + \Lambda_k\), that is introduced in section 5.7.3 where \(\H_{ij}\) is the \(400 \times 400\) diagonal block submatrix \((\H_{ij})_{ab,cd} := (\H)_{ijab,ijcd}\) and \(\Lambda_k\) is an invertible diagonal precision matrix. Equation (5.17) can be used to write \(\Lijk\) in matrix form as

\[\begin{equation} \Lijk = \H_{ij} - \lambda_w \I + \Lk = N_{ij} \Qij- N_{ij} \qij \qij^{\mathrm{T}} + \Lk \,. \tag{5.18} \end{equation}\]

Owing to eqs. (3.7) and (3.13), \(\sum_{a,b=1}^{20} q'_{ijab} = 1\). The previous equation (5.18) facilitates the calculation of the inverse of this matrix using the Woodbury identity for matrices

\[\begin{equation} (\mathbf{A} + \mathbf{B} \mathbf{D}^{-1} \mathbf{C})^{-1} = \mathbf{A}^{-1} - \mathbf{A}^{-1} \mathbf{B} (\mathbf{D} + \mathbf{C} \mathbf{A}^{-1} \mathbf{B}) ^{-1} \mathbf{C} \mathbf{A}^{-1} \;. \end{equation}\]

by setting

\[\begin{align} \mathbf{A} &= N_{ij} \Qij + \Lk \nonumber\\ \mathbf{B} &= \qij \nonumber\\ \mathbf{C} &= \qij^\mathrm{T} \nonumber\\ \mathbf{D} &=- N_{ij}^{-1} \nonumber \end{align}\]

Now, the inverse of \(\Lijk\) can be computed as

\[\begin{align} \left( \H_{ij} - \lambda_w \I + \Lk \right)^{-1} & = \mathbf{A}^{-1} - \mathbf{A}^{-1} \qij \left( -N_{ij}^{-1} + \qij^\mathrm{T} \mathbf{A}^{-1} \qij \right)^{-1} \qij^\mathrm{T} \mathbf{A}^{-1} \nonumber\\ & = \mathbf{A}^{-1} + \frac{ (\mathbf{A}^{-1} \qij) (\mathbf{A}^{-1} \qij)^{\mathrm{T}} }{ N_{ij}^{-1} - \qij^\mathrm{T} \mathbf{A}^{-1} \qij} \,. \tag{5.19} \end{align}\]

Note that \(\mathbf{A}\) is diagonal as \(\Qij\) and \(\Lk\) are diagonal matrices: \(\mathbf{A} = \text{diag}(N_{ij} q'_{ijab} + (\Lk)_{ab,ab})\). Moreover, \(\mathbf{A}\) has only positive diagonal elements, because \(\Lk\) is invertible and has only positive diagonal elements and because \(q'_{ijab} = p(x_i \eq a, x_j \eq b | \v^*,\w^*) \ge 0\). Therefore \(\mathbf{A}\) is invertible: \(\mathbf{A}^{-1} = \text{diag}(N_{ij} q'_{ijab} + (\Lk)_{ab,ab} )^{-1}\). Because \(\sum_{a,b=1}^{20} q'_{ijab} = 1\), the denominator of the second term is

\[\begin{equation} N_{ij}^{-1} - \sum_{a,b=1}^{20} \frac{{q'}_{ijab}^2}{N_{ij} q'_{ijab} + {(\Lk)}_{ab,ab} } > N_{ij}^{-1} - \sum_{a,b=1}^{20} \frac{{q'}^2_{ijab}}{N_{ij} q'_{ijab}} = 0 \end{equation}\]

and therefore the inverse of \(\Lijk\) in eq. (5.19) is well defined. The log determinant of \(\Lijk\) is necessary to compute the ratio of Gaussians (see equation (5.14)) and can be computed using the matrix determinant lemma:

\[\begin{equation} \det(\mathbf{A} + \mathbf{uv}^\mathrm{T}) = (1+\mathbf{v}^\mathrm{T} \mathbf{A}^{-1} \mathbf{u}) \det(\mathbf{A}) \end{equation}\]

Setting \(\mathbf{A} = N_{ij} \Qij + \Lk\) and \(\v = \qij\) and \(\mathbf{u} = - N_{ij} \qij\) yields

\[\begin{equation} \det(\Lijk ) = \det(\H_{ij} - \lambda_w \I + \Lk) = (1 - N_{ij}\qij^\mathrm{T} \mathbf{A}^{-1}\qij) \det(\mathbf{A}) \,. \end{equation}\]

\(\mathbf{A}\) is diagonal and has only positive diagonal elements so that \(\log(\det(\mathbf{A})) = \sum \log \left( \text{diag}(\mathbf{A}) \right)\).

5.7.7 The gradient of the log likelihood with respect to \(\muk\)

By applying the formula \(d f(x) / dx = f(x) \, d \log f(x) / dx\) to compute the gradient of eq. (5.33) (neglecting the regularization term) with respect to \(\mu_{k,ab}\), one obtains

\[\begin{equation} \frac{\partial}{\partial \mu_{k,ab}} L\!L(\mathbf{\mu}, \mathbf{\Lambda}, \gamma_k) = \sum_{1\le i<j\le L} \frac{ g_{k}(\cij) \frac{ \Gauss ( \mathbf{0} | \muk, \Lk^{-1})}{\Gauss( \mathbf{0} | \muijk, \Lijk^{-1})} \frac{\partial}{\partial \mu_{k,ab}} \log \left( \frac{ \Gauss(\mathbf{0} | \muk, \Lk^{-1})}{\Gauss( \mathbf{0} | \muijk, \Lijk^{-1})} \right) } { \sum_{k'=0}^K g_{k'}(\cij) \, \frac{ \Gauss(\mathbf{0} | \muk', \Lk'^{-1})}{\Gauss( \mathbf{0} | \muijk, \Lijk^{-1})} } . \tag{5.20} \end{equation}\]

To simplify this expression, we define the responsibility of component \(k\) for the posterior distribution of \(\wij\), the probability that \(\wij\) has been generated by component \(k\):

\[\begin{align} p(k|ij) = \frac{ g_{k}(\cij) \frac{ \Gauss( \mathbf{0} | \muk, \Lk^{-1})}{\Gauss(\mathbf{0} | \muijk, \Lijk^{-1})} } {\sum_{k'=0}^K g_{k'}(\cij) \frac{ \Gauss(\mathbf{0} | \muk', \Lk'^{-1})}{\Gauss( \mathbf{0} | \muijk', \Lijk'^{-1})} } \,. \tag{5.21} \end{align}\]

By substituting the definition for responsibility, (5.20) simplifies

\[\begin{equation} \frac{\partial}{\partial \mu_{k,ab}} L\!L(\mathbf{\mu}, \mathbf{\Lambda}, \gamma_k) = \sum_{1\le i<j\le L} p(k | ij) \frac{\partial}{\partial \mu_{k,ab}} \log \left( \frac{ \Gauss(\mathbf{0} | \muk, \Lk^{-1})}{\Gauss( \mathbf{0} | \muijk, \Lijk^{-1})} \right) , \tag{5.22} \end{equation}\]

and analogously for partial derivatives with respect to \(\Lambda_{k,ab,cd}\). The partial derivative inside the sum can be written

\[\begin{equation} \frac{\partial}{\partial \mu_{k,ab}} \log \left( \frac{ \Gauss(\mathbf{0} | \muk, \Lk^{-1})}{\Gauss( \mathbf{0} | \muijk, \Lijk^{-1})} \right) = \frac{1}{2} \frac{\partial}{\partial \mu_{k,ab}} \left( \log | \Lk | - \muk^\mathrm{T} \Lk \muk - \log | \Lijk | + \muijk^\mathrm{T} \Lijk \muijk \right)\,. \end{equation}\]

Using the following formula for a matrix \(\mathbf{A}\), a real variable \(x\) and a vector \(\mathbf{y}\) that depends on \(x\),

\[\begin{equation} \frac{\partial}{\partial x} \left( \mathbf{y}^\mathrm{T} \mathbf{A} \mathbf{y} \right) = \frac{\partial \mathbf{y}^\mathrm{T}}{\partial x} \mathbf{A} \mathbf{y} + \mathbf{y}^\mathrm{T} \mathbf{A} \frac{\partial \mathbf{y}}{\partial x} = \mathbf{y}^\mathrm{T} (\mathbf{A} + \mathbf{A}^\mathrm{T}) \frac{\partial \mathbf{y}}{\partial x} \tag{5.23} \end{equation}\]

the partial derivative therefore becomes

\[\begin{align} \frac{\partial}{\partial \mu_{k,ab}} \log \left( \frac{ \Gauss(\mathbf{0} | \muk, \Lk^{-1})}{\Gauss( \mathbf{0} | \muijk, \Lijk^{-1})} \right) =& \left( -\muk^\mathrm{T} \Lk \mathbf{e}_{ab} \, + \muijk^\mathrm{T} \Lijk \Lijk^{-1} \Lk \mathbf{e}_{ab} \right) \nonumber \\ =& \, \mathbf{e}^\mathrm{T}_{ab} \Lk ( \muijk - \muk ) \; . \end{align}\]

Finally, the gradient of the log likelihood with respect to \(\mathbf{\mu}\) becomes

\[\begin{align} \nabla_{\muk} L\!L(\mathbf{\mu}, \mathbf{\Lambda}, \gamma_k) = \sum_{1\le i<j\le L} p(k|ij) \, \Lk \left( \muijk - \muk \right) \; . \tag{5.24} \end{align}\]

The correct computation of the gradient \(\nabla_{\muk} L\!L(\mathbf{\mu}, \mathbf{\Lambda}, \gamma_k)\) has been verified using finite differences.

5.7.8 The gradient of the log likelihood with respect to \(\Lk\)

Analogously to eq. (5.22) one first needs to solve

\[\begin{align} & \frac{\partial}{\partial \Lambda_{k,ab,cd}} \log \frac{\Gauss( \mathbf{0} | \muk, \Lk^{-1})}{\Gauss( \mathbf{0} | \muijk, \Lijk^{-1})} \nonumber\\ &= \frac{1}{2} \frac{\partial}{\partial \Lambda_{k,ab,cd}} \left( \log |\Lk| - \muk^\mathrm{T} \Lk \muk - \log |\Lijk| + \muijk^\mathrm{T} \Lijk \muijk \right) \,, \tag{5.25} \end{align}\]

by applying eq. (5.23) as before as well as the formulas

\[\begin{align} \frac{\partial}{\partial x} \log |\mathbf{A} | &= \text{Tr}\left( \mathbf{A}^{-1} \frac{\partial \mathbf{A}}{\partial x} \right) , \nonumber\\ \frac{\partial \mathbf{A}^{-1}}{\partial x} &= - \mathbf{A}^{-1} \frac{\partial \mathbf{A}}{\partial x} \mathbf{A}^{-1} \,. \end{align}\]

This yields

\[\begin{align} \frac{\partial}{\partial \Lambda_{k,ab,cd}} \log |\Lk| &= \text{Tr} \left( \Lk^{-1} \frac{\partial \Lk}{\partial \Lambda_{k,ab,cd}} \right) = \text{Tr} \left( \Lk^{-1} \mathbf{e}_{ab} \mathbf{e}_{cd}^\mathrm{T} \right) = \Lambda^{-1}_{k,cd,ab} \\ \frac{\partial}{\partial \Lambda_{k,ab,cd}} \log |\Lijk| &= \text{Tr} \left( \Lijk^{-1} \frac{\partial (\H_{ij} - \lambda_w \I + \Lk)}{\partial \Lambda_{k,ab,cd}} \right) = \Lambda^{-1}_{ij,k,cd,ab} \\ \frac{\partial (\muk^\mathrm{T} \Lk \muk)}{\partial \Lambda_{k,ab,cd}} &= \muk^\mathrm{T} \mathbf{e}_{ab} \mathbf{e}_{cd}^\mathrm{T} \muk = \mathbf{e}_{ab}^\mathrm{T} \muk \muk^\mathrm{T} \mathbf{e}_{cd} = (\muk \muk^\mathrm{T})_{ab,cd} \\ \frac{\partial ( \muijk^\mathrm{T} \Lijk \muijk) }{\partial \Lambda_{k,ab,cd}} =& \muijk^\mathrm{T} \frac{\partial \Lijk}{\partial \Lambda_{k,ab,cd}} \muijk + 2 \muijk^\mathrm{T} \Lijk \frac{\partial \Lijk^{-1}}{\partial \Lambda_{k,ab,cd}} (\Hij \wij^* + \Lk \muk) \nonumber\\ &+ 2 \muijk^\mathrm{T} \frac{\partial \Lk}{\partial \Lambda_{k,ab,cd}} \muk \nonumber \\ =& (\muijk \muijk^\mathrm{T} + 2 \muijk \muk^\mathrm{T})_{ab,cd} \nonumber \\ & -2 \muijk^\mathrm{T} \Lijk \Lijk^{-1} \frac{\partial \Lijk}{\partial \Lambda_{k,ab,cd}} \Lijk^{-1} (\Hij\wij^* + \Lk \muk) \nonumber \\ =& (\muijk \muijk^\mathrm{T} + 2 \muijk \muk^\mathrm{T})_{ab,cd} - 2 \muijk^\mathrm{T} \frac{\partial \Lijk}{\partial \Lambda_{k,ab,cd}} \muijk \nonumber\\ =& (- \muijk \muijk^\mathrm{T} + 2 \muijk \muk^\mathrm{T})_{ab,cd} \,. \end{align}\]

Inserting these results into eq. (5.25) yields

\[\begin{align} \frac{\partial}{\partial \Lambda_{k,ab,cd}} \log \frac{ \Gauss(\mathbf{0} | \muk, \Lk^{-1})}{\Gauss( \mathbf{0} | \muijk, \Lijk^{-1})} = \frac{1}{2} \left( \Lk^{-1} - \Lijk^{-1} - (\muijk - \muk) (\muijk - \muk)^\mathrm{T} \right)_{ab,cd}\,. \end{align}\]

Substituting this expression into the equation (5.22) analogous to the derivation of gradient for \(\mu_{k,ab}\) yields the equation

\[\begin{align} \nabla_{\Lk} L\!L(\mathbf{\mu}, \mathbf{\Lambda}, \gamma_k) = \frac{1}{2} \sum_{1\le i<j\le L} p(k|ij) \, \left( \Lk^{-1} - \Lijk^{-1} - (\muijk - \muk) (\muijk - \muk)^\mathrm{T} \right). \tag{5.26} \end{align}\]

The correct computation of the gradient \(\nabla_{\Lk} L\!L(\mathbf{\mu}, \mathbf{\Lambda}, \gamma_k)\) has been verified using finite differences.

5.7.9 The gradient of the log likelihood with respect to \(\gamma_k\)

With \(\cij \in \{0,1\}\) defining a residue pair in physical contact or not in contact, the mixing weights can be modelled as a softmax function according to eq. (5.6). The derivative of the mixing weights \(g_k(\cij)\) is:

\[\begin{eqnarray} \frac{\partial g_{k'}(\cij)} {\partial \gamma_k} = \left\{ \begin{array}{lr} g_k(\cij) (1 - g_k(\cij)) & : k' = k\\ g_{k'}(\cij) - g_k(\cij) & : k' \neq k \end{array} \right. \end{eqnarray}\]

The partial derivative of the likelihood function with respect to \(\gamma_k\) is:

\[\begin{align} \frac{\partial} {\partial \gamma_k} L\!L(\mathbf{\mu}, \mathbf{\Lambda}, \gamma_k) =& \sum_{1\le i<j\le L} \frac{\sum_{k'=0}^K \frac{\partial}{\partial \gamma_k} g_{k'}(\cij) \frac{\Gauss(\mathbf{0} | \muk, \Lk^{-1})}{\Gauss( 0 | \muijk, \Lijk^{-1})}} {\sum_{k'=0}^K g_{k'}(\cij) \frac{ \Gauss(\mathbf{0} | \muk, \Lk^{-1})}{\Gauss( \mathbf{0} | \muijk, \Lijk^{-1})}} \nonumber \\ =& \sum_{1\le i<j\le L} \frac{\sum_{k'=0}^K g_{k'}(\cij) \frac{ \Gauss(\mathbf{0} | \muk, \Lk^{-1})}{\Gauss( \mathbf{0} | \muijk, \Lijk^{-1})} \cdot \begin{cases} 1-g_k(\cij) & \text{if } k' = k \\ -g_k(\cij) & \text{if } k' \neq k \end{cases}} {\sum_{k'=0}^K g_{k'}(\cij) \frac{ \Gauss(\mathbf{0} | \muk, \Lk^{-1})}{\Gauss( \mathbf{0} | \muijk, \Lijk^{-1})}} \nonumber\\ =& \sum_{1\le i<j\le L} \sum_{k'=0}^K p(k'|ij) \begin{cases} 1-g_k(\cij) & \text{if } k' = k \\ -g_k(\cij) & \text{if } k' \neq k \end{cases} \nonumber\\ =& \sum_{1 \leq i<j\leq L} p(k|ij) - g_k(\cij) \sum_{k'=0}^K p(k'|ij) \nonumber\\ =& \sum_{1 \leq i<j\leq L} p(k|ij) - g_k(\cij) \end{align}\]

5.7.10 Extending the Bayesian Statistical Model for the Prediction of Protein Residue-Residue Distances

It is straightforward to extend the Baysian model for contact prediction presented in section 5.1 for distances. The prior over couplings will modelled using distance dependent mixture weights \(g_k(\cij)\). Therefore eq. (5.4) is modified such that mixture weights \(g_k(\cij)\) are modelled as softmax over linear functions \(\gamma_k(\cij)\) (see Figure 5.15:

\[\begin{align} g_k(\cij) &= \frac{\exp \gamma_k(\cij)}{\sum_{k'=0}^K \exp \gamma_{k'}(\cij)} \, , \\ \gamma_k(\cij) &= - \sum_{k'=0}^{k} \alpha_{k'} ( \cij - \rho_{k'}) . \tag{5.27} \end{align}\]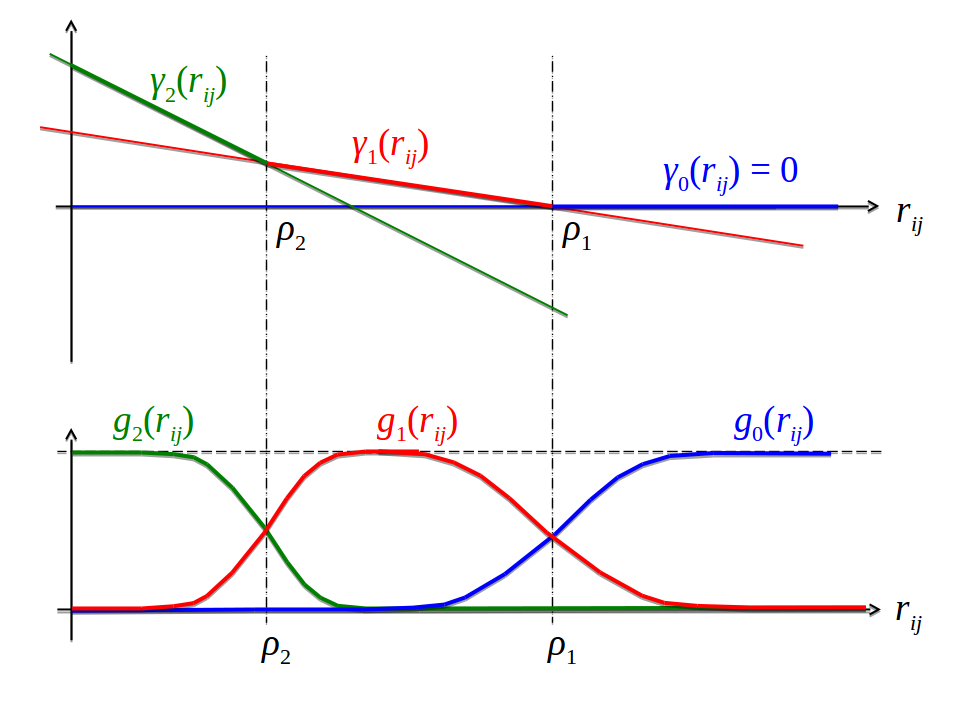

Figure 5.15: The Gaussian mixture coefficients \(g_k(\cij)\) of \(p(\wij|\cij)\) are modelled as softmax over linear functions \(\gamma_k(\cij)\). \(\rho_k\) sets the transition point between neighbouring components \(g_{k-1}(\cij)\) and \(g_k(\cij)\), while \(\alpha_k\) quantifies the abruptness of the transition between \(g_{k-1}(\cij)\) and \(g_k(\cij)\).

The functions \(g_k(\cij)\) remain invariant when adding an offset to all \(\gamma_k(\cij)\). This degeneracy can be removed by setting \(\gamma_0(\cij) \eq 0\) (i.e., \(\alpha_0 \eq 0\) and \(\rho_0 \eq 0\)). Further, the components are ordered, \(\rho_1> \ldots > \rho_K\) and it is demanded that \(\alpha_k > 0\) for all \(k\). This ensures that for \(\cij \rightarrow \infty\) we will obtain \(g_0(\cij) \rightarrow 1\) and hence \(p(\w | \X) \rightarrow \Gauss(0, \sigma_0^2 \I )\).

The parameters \(\rho_k\) mark the transition points between the two Gaussian mixture components \(k-1\) and \(k\), i.e., the points at which the two components obtain equal weights. This follows from \(\gamma_k(\cij) - \gamma_{k-1}(r) \eq \alpha_{t} ( \cij - \rho_{t})\) and hence \(\gamma_{k-1}(\rho_k) \eq= \gamma_k(\rho_k)\). A change in \(\rho_k\) or \(\alpha_k\) only changes the behaviour of \(g_{k-1}(\cij)\) and \(g_k(\cij)\) in the transition region around \(\rho_k\). Therefore, this particular definition of \(\gamma_k(\cij)\) makes the parameters \(\alpha_k\) and \(\rho_k\) as independent of each other as possible, rendering the optimisation of these parameters more efficient.

5.7.10.1 The derivative of the log likelihood with respect to \(\rho_k\)

Analogous to the derivations of \(\muk\) in section 5.7.7 and \(\Lk\) in section 5.7.8, the partial derivative with respect to \(\rho_k\) is

\[\begin{equation} \frac{\partial} {\partial \rho_k} L\!L(\mathbf{\mu}, \mathbf{\Lambda}, \rho, \alpha) = \sum_{1\le i<j\le L} \, \sum_{k'=0}^K p(k'|ij) \, \frac{\partial} {\partial \rho_k} \log g_{k'}(\cij) \,. \tag{5.28} \end{equation}\] Using the definition of \(g_k(\cij)\) in eq. (5.27), we find (rember that \(\alpha_0 \eq 0\) as noted in the last section) that \[\begin{eqnarray} \frac{\partial} {\partial \rho_k} \log g_{l}(\cij) &=& \frac{\partial} {\partial \rho_k} \log \frac{\exp \left(- \sum_{k''=1}^{k'} \alpha_{k''} (\cij - \rho_{k''} ) \right) }{ \sum_{k'=0}^K \exp \left(- \sum_{k''=1}^{k'} \alpha_{k''} (\cij - \rho_{k''} ) \right) } \nonumber \\ &=& - \frac{\partial} {\partial \rho_k} \sum_{k''=1}^{l} \alpha_{k''} (\cij - \rho_{k''} ) - \frac{\partial} {\partial \rho_k} \log \sum_{k'=0}^K \exp \left(- \sum_{k''=1}^{k'} \, \alpha_{k''} (\cij - \rho_{k''} ) \right) \nonumber \\ &=& \alpha_k \, I(l \ge k) - \frac{ \sum_{k'=0}^K \frac{\partial} {\partial \rho_k} \exp (- \sum_{k''=1}^{k'} \, \alpha_{k''} (\cij - \rho_{k''} ) ) }{ \sum_{k'=0}^K \exp (- \sum_{k''=1}^{k'} \alpha_{k''} (\cij - \rho_{k''} ) ) } \nonumber \\ &=& \alpha_k \, I(l \ge k) - \frac{ \sum_{k'=0}^K \exp (- \sum_{k''=1}^{k'} \alpha_{k''} (\cij - \rho_{k''} ) ) \, \alpha_k \, I(k' \ge k) }{ \sum_{k'=0}^K \exp (- \sum_{k''=1}^{k'} \alpha_{k''} (\cij - \rho_{k''} ) ) } \nonumber \\ &=& \alpha_k \, I(l \ge k) - \frac{ \sum_{k'=0}^K \exp (\gamma_{k'}(\cij) ) \, \alpha_k \, I(k' \ge k) }{ \sum_{k'=0}^K \exp (\gamma_{k'}(\cij) ) } \nonumber \\ &=& \alpha_k \, I(l \ge k) - \sum_{k'=0}^K g_{k'}(\cij) \, \alpha_k \, I(k' \ge k) \nonumber \\ &=& \alpha_k \, \left( I(l \ge k) - \sum_{k'=k}^K g_{k'}(\cij) \right) \, . \tag{5.29} \end{eqnarray}\]

Inserting this into eq. (5.28) yields

\[\begin{align} \frac{\partial} {\partial \rho_k} L\!L(\mathbf{\mu}, \mathbf{\Lambda}, \rho, \alpha) &= \sum_{1\le i<j\le L} \, \sum_{k'=0}^K p(k'|ij) \, \alpha_k \, \left( I(k' \ge k) - \sum_{k''=k}^K g_{k''}(\cij) \right) \nonumber \\ &= \alpha_k \, \sum_{1\le i<j\le L} \, \left( \sum_{k'=k}^K p(k'|ij) - \sum _{k'=0}^K p(k'|ij) \, \sum_{k''=k}^K g_{k''}(\cij) \right) , \end{align}\]

and finally

\[\begin{equation} \frac{\partial} {\partial \rho_k} L\!L(\mathbf{\mu}, \mathbf{\Lambda}, \rho, \alpha) = \alpha_k \, \sum_{1\le i<j\le L} \, \sum_{k'=k}^K ( p(k'|ij) - g_{k'}(\cij) ) \, . \end{equation}\]

This equation has an intuitive meaning: The gradient is the difference between the summed probability mass predicted to be due to components \(k' \ge k\), \(p(k'\ge k | ij)\), and the sum of the prior probabilities \(g_k(\cij)\) for components \(k' \ge k\), where the sum runs over all training points indexed by \(i,j\).

5.7.10.2 The derivative of the log likelihood with respect to \(\alpha_k\)

Last and similar to the previous derivation, the partial derivative with respect to \(\alpha_k\) is

\[\begin{equation} \frac{\partial} {\partial \alpha_k} L\!L(\mathbf{\mu}, \mathbf{\Lambda}, \rho, \alpha) = \sum_{1\le i<j\le L} \, \sum_{k'=0}^K p(k'|ij) \, \frac{\partial} {\partial \alpha_k} \log g_{k'}(\cij) \,. \tag{5.30} \end{equation}\]

Similarly as before,

\[\begin{align} \frac{\partial} {\partial \alpha_k} \log g_{l}(\cij) &= \frac{\partial} {\partial \alpha_k} \log \frac{\exp (- \sum_{k''=1}^{l} \alpha_{k''} (\cij - \rho_{k''} ) }{ \sum_{k'=0}^K \exp (- \sum_{k''=1}^{k'} \alpha_{k''} (\cij - \rho_{k''} ) ) } \nonumber \\ &= - \frac{\partial} {\partial \alpha_k} \sum_{k''=1}^{l} \alpha_{k''} (\cij - \rho_{k''} ) - \frac{\partial} {\partial \alpha_k} \log \sum_{k'=0}^K \exp \left(- \sum_{k''=1}^{k'} \, \alpha_{k''} (\cij - \rho_{k''} ) \right) \nonumber \\ &= - (\cij - \rho_{k} ) \, I(l \ge k) - \frac{ \sum_{k'=0}^K \frac{\partial} {\partial \alpha_k} \exp (- \sum_{k''=1}^{k'} \, \alpha_{k''} (\cij - \rho_{k''} ) ) }{ \sum_{k'=0}^K \exp (- \sum_{k''=1}^{k'} \alpha_{k''} (\cij - \rho_{k''} ) ) } \nonumber \\ &= - (\cij - \rho_{k} ) \, \left( I(l \ge k) - \sum_{k''=k}^K g_{k''}(\cij) ) \right) \, . \tag{5.31} \end{align}\]

Inserting this into eq. (5.30) yields

\[\begin{align} \frac{\partial} {\partial \alpha_k} L\!L(\mathbf{\mu}, \mathbf{\Lambda}, \rho, \alpha) &= - \sum_{1\le i<j\le L} \, \sum_{k'=0}^K p(k'|ij) \, (\cij - \rho_k) \, \left( I(k' \ge k) - \sum_{k''=k}^K g_{k''}(\cij) ) \right) \nonumber \\ &= -\sum_{1\le i<j\le L} \, (\cij - \rho_k) \, \left( \sum_{k'=k}^K p(k'|ij) - \sum _{k'=0}^K p(k'|ij) \, \sum_{k''=k}^K g_{k''}(\cij) ) \right) , \end{align}\]

and finally

\[\begin{equation} \frac{\partial} {\partial \alpha_k} L\!L(\mathbf{\mu}, \mathbf{\Lambda}, \rho, \alpha) = \sum_{1\le i<j\le L} \, (\rho_k - \cij) \, \sum_{k'=k}^K ( p(k'|ij) - g_{k'}(\cij) ) \, . \end{equation}\]

5.7.11 Training the Hyperparameters in the Likelihood Function of Contact States

The model parameters \(\mathbf{\mu} = (\mathbf{\mu}_{1},\ldots,\mathbf{\mu}_K)\), \(\mathbf{\Lambda} = (\mathbf{\Lambda}_1,\ldots,\mathbf{\Lambda}_K)\) and \(\mathbf{\gamma} = (\mathbf{\gamma}_1,\ldots,\mathbf{\gamma}_K)\) will be trained by maximizing the logarithm of the full likelihood over a set of training MSAs \(\X^1,\ldots,\X^N\) and associated structures with \(\c^1,\ldots,\c^M\) plus a regularizer \(R(\mathbf{\mu}, \mathbf{\Lambda})\):

\[\begin{equation} L\!L(\mathbf{\mu}, \mathbf{\Lambda}, \mathbf{\gamma}) + R(\mathbf{\mu}, \mathbf{\Lambda}) = \sum_{n=1}^M \log p(\X^m | \c^m, \mathbf{\mu}, \mathbf{\Lambda}, \mathbf{\gamma} ) + R(\mathbf{\mu}, \mathbf{\Lambda}) \rightarrow \max \, . \end{equation}\]

The regulariser penalizes values of \(\muk\) and \(\Lk\) that deviate too far from zero:

\[\begin{align} R(\mathbf{\mu}, \mathbf{\Lambda}) = -\frac{1}{2 \sigma_{\mu}^2} \sum_{k=1}^K \sum_{ab=1}^{400} \mu_{k,ab}^2 -\frac{1}{2 \sigma_\text{diag}^2} \sum_{k=1}^K \sum_{ab=1}^{400} \Lambda_{k,ab,ab}^2 \tag{5.32} \end{align}\]

Reasonable values are \(\sigma_{\mu}=0.1\), \(\sigma_\text{diag} = 100\).
These values have been chosen empirically, so that regularization does not substantially impact the strength of hyperparameters but does prevent components with small weights from wandering off zero too far or from becoming too narrow. It has been found that this is necessary especially for mixtures with many components.

The log likelihood can be optimized using L-BFGS-B [238], which requires the computation of the gradient of the log likelihood. For simplicity of notation, the following calculations consider the contribution of the log likelihood for just one protein, which allows to drop the index \(m\) in \(\cij^m\), \((\wij^m)^*\) and \(\Hij^m\). From eq. (5.14) the log likelihood for a single protein is

\[\begin{equation} L\!L(\mathbf{\mu}, \mathbf{\Lambda}, \gamma_k) = \sum_{1 \le i < j \le L} \log \sum_{k=0}^K g_{k}(\cij) \frac{\Gauss( \mathbf{0} | \muk, \Lk^{-1})}{\Gauss(\mathbf{0} | \muijk, \Lijk^{-1})} + R(\mathbf{\mu}, \mathbf{\Lambda}) + \text{const.}\,. \tag{5.33} \end{equation}\]

For the optimization, I used the module optimize.minimize from the Python package SciPy (v 0.19.1) and the flag method="L-BFGS-B". According to the default setting, optimization will converge when (f^k - f^{k+1})/max{|f^k|,|f^{k+1}|,1} <= ftol with ftol=2.220446049250313e-09.

The negative log likelihood will be monitored during optimization. Every ten iterations it will be evaluated on a validation set of 1000 residue pairs per contact class to ensure that the model is not overfitting the training data.

5.7.11.1 Dataset Specifications

An equal number of residue pairs that are in physical contact \(\Delta\Cb <8 \angstrom\) and are not in contact \(\Delta\Cb >8 \angstrom\) is selected according to the following criteria:

• contact: \(\Delta\Cb <8 \angstrom\)
• non-contact: \(\Delta\Cb >8 \angstrom\) or \(\Delta\Cb >20 \angstrom\)
• diversity (\(\frac{\sqrt{N}}{L}\)) > 0.3
• percentage of gaps per column \(\leq 0.5\)
• number of non-gapped sequences at position \(i\) and \(j\), \(N_{ij} > 1\)
• maximum number of contacts selected per protein = 500
• maximum number of non-contacts selected per protein = 1000
• number residue pairs for contacts (\(\cij \eq 1\)) and
  non-contacts (\(\cij \eq 0\)) \(\in \{10000, 100000, 30000, 500000 \}\)

Proteins from subsets 1-5 of the dataset described in method section 2.6.1 have been used for training. Proteins are randomly selected and before residue pairs are selected from a protein, they are shuffled to avoid position bias. The validation set is generated according to the same criteria and constitutes 1000 residue pairs per contact class.

The MAP estimates of the coupling parameters \(\wij^*\) that are needed to compute the Hessian \(\Hij\) as descibed in method section 5.7.5 are computed by maximizing the pseudo-likelihodd and by maximizing the full likelihood with contrastive divergence. Stochastic gradient descent using the tuned hyperparameters presented in chapter 3 will be used to optimize the full likelihood with contrastive divergence. The ADAM optimizer is not used because its adaptive learning rates violate the condition \(\sum_{a,b}^{20} \wijab = 0\) which is described in section 3.4.1.

For validation of the models, 500 proteins are randomly selected from subsets 6-8 of the dataset described in method section 2.6.1.

5.7.11.2 Model Specifications

The mixture weights \(g_k(\cij)\) are randomly sampled from a uniform distribution over the half-open interval [0, 1) and normalized so that \(\sum_k^K g_k(\cij) = 1\) for \(\cij=0\) and \(\cij=1\), respectively. Subsequently, the \(g_k(\cij)\) are reparameterized as softmax functions as given in eq. (5.6) and fixing \(\gamma_0(\cij)=0\) to avoid overparametrization.

The 400 dimensional \(\muk\) vectors for \(k \in \{1, \ldots, K\}\) are initialized from 400 random draws from a normal distribution with zero mean and standard deviation \(\sigma \eq 0.05\). The zeroth component is kept fixed at zero (\(\mathbf{\mu_0} \eq 0\)) and will not be optimized.

The precision matrices \(\Lk\) will be modelled as diagonal matrices, setting all off-diagonal elements to zero. The 400 diagonal elements \((\Lk)_{ab, ab}\) for \(k \in \{1, \ldots, K\}\) are initialized from 400 random draws from a normal distribution with zero mean and standard deviation \(\sigma \eq 0.005\). The 400 diagonal elements of the precision matrix for the zeroth component \(\mathbf{\Lambda_0}\) are initialized as 400 random draws from a normal distribution with zero mean and standard deviation \(\sigma \eq 0.0005\). Therefore, the zeroth component is sharply centered at zero. Furthermore, the diagonals of the precision matrices are reparameterized as \((\Lk)_{ab, ab} = \exp((\Lk)_{ab, ab}^{\prime})\) in order to ensure that the values stay positive. Gradients for \(\Lk\) derived in next sections have been adapted according to this reparametrization.

The number of model parameters assembles as follows:

• \((K-1) \times 400\) parameters for \(\muk\) with \(k \in \{1, \ldots, K \}\) (\(\mu_0 = 0\))
• \(K \times 400\) parameters for the diagonal \((\Lk)_{ab, ab}\) with \(k \in \{0, \ldots, K\}\)
• \(2 \times (K\!-\!1)\) parameters for \(\gamma_k(\cij)\) for \(k \in \{1,2\}\) and \(\cij \in \{0,1\}\) (\(\gamma_0(\cij)\eq1\)).

This yields 2004 parameters for \(K\eq3\) Gaussian components, 3608 parameters for \(K\eq5\) and 7618 parameters for \(K\eq10\) components.

References

94. Murphy, K.P. (2012). Machine Learning: A Probabilistic Perspective (MIT Press).

238. Byrd, R.H., Lu, P., Nocedal, J., and Zhu, C. (1995). A Limited Memory Algorithm for Bound Constrained Optimization. SIAM J. Sci. Comput. 16, 1190–1208., doi: 10.1137/0916069.