PhD thesis: residue-residue contact prediction

1.1 Biological Background

In 1972, Anfinsen and his collegues received the Nobel Prize for their research on protein folding which lead to the postulation of one of the basic principles in molecular biology, which is known as Anfinsen’s dogma: a protein’s native structure is uniquely determined by its amino acid sequence [1]. With certain exceptions (e.g. intrinsically disordered proteins [2] or prions[3]), this dogma has proven to hold true at least for globular proteins.

Ever since, it is regarded as the biggest challenge in structural bioinformatics to realiably predict a protein’s structure given only its amino acid sequence [4,5]. De novo protein structure prediction methods minimize physical or knowledge based energy functions to identify the lowest-energy conformation that generally corresponds to the native protein conformation. However, due to the high degree of conformational flexibility, the search space of possible conformations cannot be explored exhaustively for a typical protein. Given a protein with 101 residues that has 100 peptide bonds with two torsion angles each and assuming three stable conformations for each of the bond angles, there will be $3^{200} \approx 10^{95}$ configurations. This number of conformations cannot be sampled sequentially in a lifetime, even when sampling at high rates. Yet, proteins fold almost instantaneously within milliseconds. This discrepancy is known as Levinthal’s paradox [6] and limits purely de novo based protein structure prediction to small proteins.

Far more successfull are template-based modelling approaches. Given the observation that structure is more conserved than sequence in a protein family [7], the structure of a target protein can be inferred from a homologous protein [8], that is a protein of shared ancestry. The degree of structural conservation is linked to the level of pairwise sequence identity [9]. Therefore, the accuracy of a model crucially depends on the sequence identity between target and template and determines the applicability of the model [10]. By definition, homology derived models are unable to capture new folds and their main limitation lies in the availability and identification of suitable templates [11].

The number of solved protein structures increases steadily but only slowly, as experimental methods are both time consuming and expensive [11]. The Protein Data Bank (PDB) is the main repository for marcomolecular structures and currently (October 2017) holds about 135,000 atomic models of proteins [12]. The primary technique for determining protein structures is X-ray crystallography, accounting for roughly 90% of entries in the PDB. About 9% of protein structures have been solved using nuclear magnetic resonance (NMR) spectroscopy and less than 1% using electron microscopy (EM) (see left plot in Figure 1.1).

Figure 1.1: Comparing the amount of primary and tertiary protein structures over time. Left Yearly growth of protein structures in the PDB [12] by structure determination method. Right Yearly growth of database entries in the UniprotKB/TrEMBL [13], containing automatically annotated protein sequences, in the UniprotKB/SwissProt [13], containing manually curated protein sequences and in the PDB containing solved protein structures.

All three experimental techniques have advantages and limitations with respect to certain modelling aspects. X-ray crystallography involves protein overexpression, purification and crystallization and finding the the correct experimental conditions to arrive at a pure and regular crystal is a challenging and sometimes impossible task. Especially membrane proteins are difficult to study owing to their overall flexibility and hydrophobic surfaces which requires suitable detergents to extract the proteins from their membrane environment which in turn makes crystallization even more challenging [14,15]. Furthermore, the unnatural crystal environment can result in crystal-induced artifacts, like altered sidechain conformations due to crystal packing interactions [16]. In contrast, nuclear magnetic resonance (NMR) spectroscopy studies the protein in solution under physiological conditions and enables the observation of intramolecular dynamics, reaction kinetics or protein folding as ensembles of protein structures can be observed [17]. On the downside, validation of NMR-derived structure ensembles is complicated and there is an upper size limit of about 25 kDa for efficient use of the technique [18]. Recently, cryo-EM has undergone a “resolution revolution” and macromolecules have been solved to near-atomic resolutions [19,20]. Technological developments, such as better electron detectors as well as advanced image processing software has enabled high resolution structure determination and led to an exponential growth in number of structures deposited in the PDB. Cryo-EM is particularly suited to study large macromolecular complexes without the need to make crystals and therefore complements the other two structure determination techniques.

In contrast to the tedious task of determining the tertiary structure of a protein to atomic resolution, it has become very easy to decipher the primary sequence of proteins. Since the completion of the human genome in 2003, high-throughput sequencing technologies have been developed at an extraordinary pace [???]. Not only has the amount of time decreased that is needed to sequence whole genomes but also costs have been drastically reduced [21]. The price for sequencing a single genome has dropped from the US$3 billion spent by the Human Genome Project to as little as US$1,000[22]. At the beginning of 2017, Illumina announced the launch of their latest high-throughput sequencing technology, NovaSeq, which is capable of sequencing $\sim \! 48$ human genomes in parallel at 30x coverage within $\sim \! 45$ hours [23]. Advances in sequencing technologies have led to the emergence of new fields of studies, like metagenomics and single-cell genomics, that enable sequencing of microorganisms that cannot be cultured in the lab [24–26]. With these approaches the genomic coverage of the microbial world is expanding which is directly reflected in a substantial increase in novel protein families [27–29]. More than 70 000 genomes have been completely sequenced and about 90 million sequences (October 2017) have been translated into protein amino acid sequences and are stored in the UniprotKB/TrEMBL database, the leading resource for protein sequences [13,30].

The resultant gap between the number of protein structures and protein sequences is constantly widening (see right plot in Figure 1.1) despite tremendous efforts in automating experimental structure determination [5]. This trend illustrates the essential importance of computational approaches that can complement experimental structural biology efforts in order to bridge this gap. Over the last decades, template-based methods have matured to a point where they are able to generate high-resolution structural models that are routinley and conveniently used in life-science research and by the biological community [5,31]. De novo methods aiming at predicting protein structures from sequence alone are required in case no homologue template structure can be identified or the protein sequence represents a novel fold. Albeit purely de novo approaches are hampered by the combinatorial explosion of possible conformations for larger proteins, combining them with structural information from different types of experiments can help to reduce the degrees of freedom in the conformational search space [5]. Several sophisticated integrative approaches have been developed and proven to be powerful [32–34]. For example, sparse low-resolution experimental data from chemical cross-linking/mass spectroscopy or nuclear Overhauser enhancement (NOE) distance data generated from NMR experiments, provide distance restraints to guide folding to a correct structure [35–37].

Another complementary source of information is given by predicted protein residue-residue contacts. The invention of direct coupling analysis (DCA) in 2009 was a breakthrough in the development of computational methods to infer spatially close residue pairs from coevolutionary signals in the evolutionary record of protein families [38]. Since then, the field of contact prediction has experienced rapid progress and methods are continously improving. Modern contact prediction approaches produce predictions that are sufficiently accurate to successfully assist the de novo prediction of protein structures [39]. The last years have seen an enourmous wealth of studies applying predicted residue-residue contacts not only as distance constraints for de novo modelling of protein structures, but also in many different fields in structural biology, such as domain prediction [40], studying alternative conformations [41] or inferring evolutionary fitness landscapes and quantifying mutational effects [42].

It has long been known that native contacts can be used to reliably reconstruct native protein 3D structure [43]. This is because a contact map retains the full 3D structural information of a protein, eventhough it provides only a 2D represenation of the protein structure. For a protein of length $L$, a contact map is a binary $L \times L$ matrix, where the binary element in the matrix $C(i,j)$ for two residues $i$ and $j$ is given by \[\begin{equation} C(i,j) = \begin{cases} 1, & \text{if } \Delta \Cb < T \\ 0, & \text{otherwise} \end{cases} \end{equation}\]

where $\Delta \Cb$ is the euclidean distance between $\Cb$ atoms ($C_\alpha$ for glycine) of residues $i$ and $j$ and $T$ is a distance threshhold (typically 8 $\angstrom$). Figure 1.2 shows an example of a residue-residue contact map generated from a small protein domain. While it has been shown that only a small subset of native contacts is sufficient to allow accurate modelling of the protein structure, the quality of predicted residue-residue contacts crucially controls the quality of the final structural model [44,45]. Currently published DCA methods are very successful at predicting contacts for large protein families. However they all apply the same heuristics on top of the underlying statistical model thereby ignoring valuable information. It is a reasonable assumption that by making full use of the available information, the predictive performance of the models should improve and as a consequence extend the applicability of DCA methods to smaller protein families. The aim of this thesis is therefore to improve the models for residue-residue contact prediction by developing a flexible and transparent Bayesian framework that adresses these issues.

The next chapter gives an introduction to state-of-the-art contact prediction approaches, how the predicted residue-residue contacts are applied and which challenges the current methods have to face.

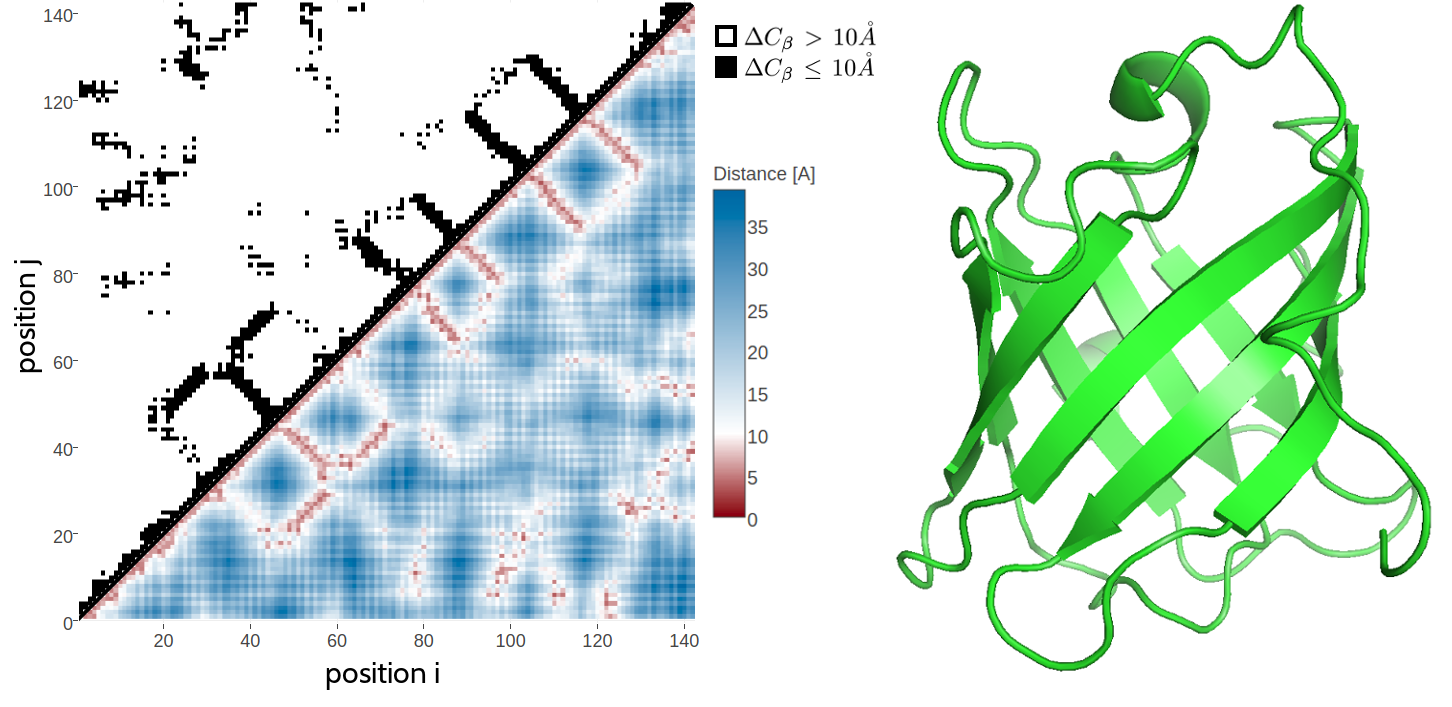
$2D and 3D representations of protein triabin, a thombin inhibitor from triatoma pallidipennis (PDB identifier 1avg chain I). Left The upper left matrix illustrates a contact map using an $10 \angstrom \Cb$ cutoff. A black square is drawn at position $(i, j)$ if the $\Cb$ atoms of residues $i$ and $j$ are closer than $10 \angstrom$ in the structure. The lower right matrix illustrates a distance map. Color reflects $\Cb$ distances between residue pairs with red colors representing $\Delta \Cb \le 10 \angstrom$ and blue colors representing $\Delta \Cb > 10 \angstrom$. Right 3D Structure showing an eight-stranded beta-barrel.$

Figure 1.2: 2D and 3D representations of protein triabin, a thombin inhibitor from triatoma pallidipennis (PDB identifier 1avg chain I). Left The upper left matrix illustrates a contact map using an $10 \angstrom \Cb$ cutoff. A black square is drawn at position $(i, j)$ if the $\Cb$ atoms of residues $i$ and $j$ are closer than $10 \angstrom$ in the structure. The lower right matrix illustrates a distance map. Color reflects $\Cb$ distances between residue pairs with red colors representing $\Delta \Cb \le 10 \angstrom$ and blue colors representing $\Delta \Cb > 10 \angstrom$. Right 3D Structure showing an eight-stranded beta-barrel.

References

1. Anfinsen, C.B. (1973). Principles that Govern the Folding of Protein Chains. Sci. (80-. ). 181, 223–230., doi: 10.1126/science.181.4096.223.

2. Wright, P.E., and Dyson, H. (1999). Intrinsically unstructured proteins: re-assessing the protein structure-function paradigm. J. Mol. Biol. 293, 321–331., doi: 10.1006/jmbi.1999.3110.

3. Fraser, P.E. (2014). Prions and prion-like proteins. J. Biol. Chem. 289, 19839–40., doi: 10.1074/jbc.R114.583492.

4. Samish, I., Bourne, P.E., and Najmanovich, R.J. (2015). Achievements and challenges in structural bioinformatics and computational biophysics. Bioinformatics 31, 146–150., doi: 10.1093/bioinformatics/btu769.

5. Schwede, T. (2013). Protein modeling: what happened to the “protein structure gap”? Structure 21, 1531–40., doi: 10.1016/j.str.2013.08.007.

6. Levinthal, C. (1969). How to Fold Graciously. 22–24.

7. Lesk, A.M., and Chothia, C. (1980). How different amino acid sequences determine similar protein structures: The structure and evolutionary dynamics of the globins. J. Mol. Biol. 136, 225–270., doi: 10.1016/0022-2836(80)90373-3.

8. Sander, C., and Schneider, R. (1991). Database of homology-derived protein structures and the structural meaning of sequence alignment. Proteins 9, 56–68., doi: 10.1002/prot.340090107.

9. Chothia, C., and Lesk, A.M. (1986). The relation between the divergence of sequence and structure in proteins. EMBO J. 5, 823–6.

10. Martí-Renom, M.A., Stuart, A.C., Fiser, A., Sánchez, R., Melo, F., and Šali, A. (2000). Comparative Protein Structure Modeling of Genes and Genomes. Annu. Rev. Biophys. Biomol. Struct. 29, 291–325., doi: 10.1146/annurev.biophys.29.1.291.

11. Dorn, M., Silva, M.B. e, Buriol, L.S., and Lamb, L.C. (2014). Three-dimensional protein structure prediction: Methods and computational strategies. Comput. Biol. Chem. 53, 251–276., doi: 10.1016/j.compbiolchem.2014.10.001.

12. Berman, H.M. (2000). The Protein Data Bank. Nucleic Acids Res. 28, 235–242., doi: 10.1093/nar/28.1.235.

13. The UniProt Consortium (2017). UniProt: the universal protein knowledgebase. Nucleic Acids Res. 45, D158–D169., doi: 10.1093/nar/gkw1099.

14. Carpenter, E.P., Beis, K., Cameron, A.D., and Iwata, S. (2008). Overcoming the challenges of membrane protein crystallography. Curr. Opin. Struct. Biol. 18, 581–6., doi: 10.1016/j.sbi.2008.07.001.

15. Moraes, I., Evans, G., Sanchez-Weatherby, J., Newstead, S., and Stewart, P.D.S. (2014). Membrane protein structure determination - the next generation. Biochim. Biophys. Acta 1838, 78–87., doi: 10.1016/j.bbamem.2013.07.010.

16. Jacobson, M.P., Friesner, R.A., Xiang, Z., and Honig, B. (2002). On the Role of the Crystal Environment in Determining Protein Side-chain Conformations. J. Mol. Biol. 320, 597–608., doi: 10.1016/S0022-2836(02)00470-9.

17. Bieri, M., Kwan, A.H., Mobli, M., King, G.F., Mackay, J.P., and Gooley, P.R. (2011). Macromolecular NMR spectroscopy for the non-spectroscopist: beyond macromolecular solution structure determination. FEBS J. 278, 704–715., doi: 10.1111/j.1742-4658.2011.08005.x.

18. Billeter, M., Wagner, G., and Wüthrich, K. (2008). Solution NMR structure determination of proteins revisited. J. Biomol. NMR 42, 155–8., doi: 10.1007/s10858-008-9277-8.

19. Egelman, E.H. (2016). The Current Revolution in Cryo-EM. Biophysj 110, 1008–1012., doi: 10.1016/j.bpj.2016.02.001.

20. Fernandez-Leiro, R., and Scheres, S.H.W. (2016). Unravelling biological macromolecules with cryo-electron microscopy. Nature 537, 339–46., doi: 10.1038/nature19948.

21. Reuter, J.A., Spacek, D.V., and Snyder, M.P. (2015). High-throughput sequencing technologies. Mol. Cell 58, 586–97., doi: 10.1016/j.molcel.2015.05.004.

22. Goodwin, S., McPherson, J.D., and McCombie, W.R. (2016). Coming of age: ten years of next-generation sequencing technologies. Nat. Rev. Genet. 17, 333–351., doi: 10.1038/nrg.2016.49.

23. NovaSeq System Specifications | The next era of sequencing starts now.

24. Tringe, S.G., and Rubin, E.M. (2005). Metagenomics: DNA sequencing of environmental samples. Nat. Rev. Genet. 6, 805–814., doi: 10.1038/nrg1709.

26. Wooley, J.C., Godzik, A., and Friedberg, I. (2010). A primer on metagenomics. PLoS Comput. Biol. 6, e1000667., doi: 10.1371/journal.pcbi.1000667.

27. Rinke, C., Schwientek, P., Sczyrba, A., Ivanova, N.N., Anderson, I.J., Cheng, J.-F., Darling, A., Malfatti, S., Swan, B.K., and Gies, E.A. et al. (2013). Insights into the phylogeny and coding potential of microbial dark matter. Nature 499, 431–437., doi: 10.1038/nature12352.

29. Forster, S.C. (2017). Illuminating microbial diversity. Nat. Rev. Microbiol. 15, 578–578., doi: 10.1038/nrmicro.2017.106.

30. Zerihun, M.B., and Schug, A. (2017). Biomolecular coevolution and its applications: Going from structure prediction toward signaling, epistasis, and function. Biochem. Soc. Trans., BST20170063., doi: 10.1042/BST20170063.

31. Dukka, B.K. (2016). Recent advances in sequence-based protein structure prediction. Brief. Bioinform. 31, 1–12., doi: 10.1093/bib/bbw070.

32. Ornes, S. (2016). Let the structural symphony begin. Nature 536, 361–363., doi: 10.1038/536361a.

34. Tang, Y., Huang, Y.J., Hopf, T.A., Sander, C., Marks, D.S., and Montelione, G.T. (2015). Protein structure determination by combining sparse NMR data with evolutionary couplings. Nat. Methods advance on.

35. Li, W., Zhang, Y., and Skolnick, J. (2004). Application of sparse NMR restraints to large-scale protein structure prediction. Biophys. J. 87, 1241–8., doi: 10.1529/biophysj.104.044750.

37. Rappsilber, J. (2011). The beginning of a beautiful friendship: cross-linking/mass spectrometry and modelling of proteins and multi-protein complexes. J. Struct. Biol. 173, 530–40., doi: 10.1016/j.jsb.2010.10.014.

38. Weigt, M., White, R.A., Szurmant, H., Hoch, J.A., and Hwa, T. (2009). Identification of direct residue contacts in protein-protein interaction by message passing. Proc. Natl. Acad. Sci. U. S. A. 106, 67–72., doi: 10.1073/pnas.0805923106.

39. Marks, D.S., Colwell, L.J., Sheridan, R., Hopf, T.A., Pagnani, A., Zecchina, R., and Sander, C. (2011). Protein 3D structure computed from evolutionary sequence variation. PLoS One 6, e28766., doi: 10.1371/journal.pone.0028766.

40. Sadowski, M.I. (2013). Prediction of protein domain boundaries from inverse covariances. Proteins 81, 253–260., doi: 10.1002/prot.24181.

41. Parisi, G., Zea, D.J., Monzon, A.M., and Marino-Buslje, C. (2015). Conformational diversity and the emergence of sequence signatures during evolution. Curr. Opin. Struct. Biol. 32C, 58–65.

42. Hopf, T.A., Ingraham, J.B., Poelwijk, F.J., Schärfe, C.P.I., Springer, M., Sander, C., and Marks, D.S. (2017). Mutation effects predicted from sequence co-variation. Nat. Biotechnol. 35, 128–135., doi: 10.1038/nbt.3769.

43. Vendruscolo, M., Kussell, E., and Domany, E. (1997). Recovery of protein structure from contact maps. Fold. Des. 2, 295–306., doi: 10.1016/S1359-0278(97)00041-2.

44. Kim, D.E., Dimaio, F., Yu-Ruei Wang, R., Song, Y., and Baker, D. (2014). One contact for every twelve residues allows robust and accurate topology-level protein structure modeling. Proteins 82 Suppl 2, 208–18.

45. Duarte, J.M., Sathyapriya, R., Stehr, H., Filippis, I., and Lappe, M. (2010). Optimal contact definition for reconstruction of contact maps. BMC Bioinformatics 11., doi: 10.1186/1471-2105-11-283.