1.5 Challenges for Coevolutionary Inference

Coevolution methods face several challenges when interpreting the covariation signals obtained from a MSA. Some of these challenges have been successfully met (e.g. disentangling transitive effects with global statistical models), others are still open or open up new perspectives, such as dissecting different sources of coevolution signals.

1.5.1 Phylogenetic Effects as a Source of Noise

Sequences in MSAs do not represent independent samples of a protein family. In fact, there is selection bias from sequencing species of special interest (e.g human pathogens) or sequencing closely related species, e.g multiple strains. This uneven sampling of a protein family’s sequence space leaves certain regions unexplored whereas others are statistically overrepresented [95,96,178]. Furthermore, due to their evolutionary relationship, sequences of a protein family have a complicated dependence structure. Closely related sequences can cause spurious correlations between positions, as there was not sufficient time for the sequences to diverge from their common ancestor [58,62,63]. Figure 1.10 illustrates a simplified example, where dependence of sequences due to phylogeny leads to a covariation signal.

To reduce the effects of overrepresented sequences, typically a simple weighting strategy is applied that assigns a weight to each sequence that is the inverse of the number of similar sequences according to an identity threshold [99]. It has been found that reweighting improves contact prediction performance [65,95,179] significantly but results are robust against the choice of the identity threshold in a range between 0.7 and 0.9 [95].

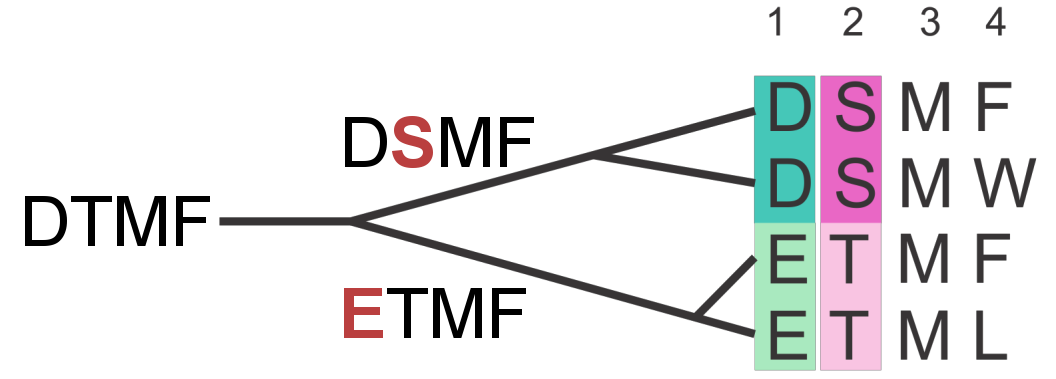
Figure 1.10: The phylogenetic dependence of closely related sequences can produce covariation signals. Here, two independent mutation events (highlighted in red) in two branches of the tree result in a perfect covariation signal for two positions.

1.5.2 Entropic Effects as a Source of Noise

Another source for noise is entropy bias that is closely linked to phylogenetic effects. By nature, methods detecting signals from correlated mutations rely on a certain degree of covariation between sequence positions [63]. Highly conserved interactions pose a conceptual challenge, as changes from one amino acid to another cannot be detected if sequences do not vary. This results in generally higher co-evolution signals from positions with high entropy and underestimated signals for highly conserved interactions [56]. Several heuristics have been proposed to reduce entropy effects, such as Row-Column-Weighting (RCW) [58] or Average Product Correction (APC) [59] (see section 1.2.4.6).

1.5.3 Finite Sampling Effects

Spurious correlations can arise from random statistical noise and blur true co-evolution signals especially in low data scenarios. Consequently, false positive predictions attributable to random noise accumulate for protein families comprising low numbers of homologous sequences. This relationship was confirmed in many studies and as a rule of thumb it has been argued that proteins with \(L\) residues need at least 5L sequences in order to obtain confident predictions that can bet used for protein structure prediction [102,178]. Recently it was shown that precision of predicted contacts saturates for protein families with more than \(10^3\) diverse sequences and that precision is only dependent on protein length for families with small number of sequences [177].

Interesting targets for contact prediction are protein families without any associated structural information. As can be seen in Figure 1.11, those protein families generally comprise low numbers of homologous sequences with a median of 185 sequences per family and are thus susceptible to finite sampling effects.

With the rapidly increasing size of protein sequence databases (see section 1.1) the number of protein families with enough sequences for accuarate contact predictions will increase steadily [102,180]. Nevertheless, because of the already mentioned sequencing biases, better and more sensitive statistical models are indespensible to extend the applicability domain of coevolutionary methods.

Figure 1.11: Distribution of PFAM family sizes. Less than half of the families in PFAM (7990 compared to 8489 families) do not have an annotated structure. The median family size in number of sequences for families with and without annotated structures is 185 and 827 respectively. Data taken from PFAM 31.0 (March 2017, 16712 entries) [181].

1.5.4 Multiple Sequence Alignments

A correct MSA is the essential starting point for coevolution analysis as incorrectly aligned residues will confound the true signal. Highly sensitive and accurate alignment tools such as HHblits generate high quality alignments suitable for contact prediction [182]. However, there are certain subtleties to be kept in mind when generating alignments.

For example, proteins with repeated stretches of amino acids or with regions of low complexity are notoriously hard to align. Especially, repeat proteins have been found to produce many false positive contact predictions [177]. Therefore, MSAs need to be generated with great care and covariation methods need to be tailored to these specific types of proteins [183,184].

Furthermore, sensitivity of sequence search is critically dependent on the research question at hand and on the protein family under study. Many diverse sequences in general increase precision of predictions [174,185]. However, deep alignments can capture coevolutionary signals from different subfamilies [149]. If only a specific subfamily is of interest, many false predictions might arise from strong coevolutionary signals specific to another subfamily that constitutes a prominent subset in the alignment [169]. Therefore, a trade-off between specificity and diversity of the alignment is required to reach optimal results [119].

Another intrinsic characteristic of MSAs are repeated stretches of gaps that result from commonly utilized gap-penalty schemes assigning large penalties to insert a gap and lower penalties to gap extensions. Most statistical coevolution models for contact prediction treat gaps as the 21st amino acid. This introduces an imbalance as gaps and amino acids express different behaviours which can result in gap-induced artefacts [110].

1.5.5 Alternative Sources of Coevolution

Coevolutionary signals can not only arise from intra-domain contacts, but also from other sources, like homo-oligomeric contacts, alternative conformations, ligand-mediated interactions or even contacts over hetero-oligomeric interfaces (see Figure 1.12) [178]. With the objective to predict physical contacts it is therefore necessary to identify and filter these alternative sources of coevolutionary couplings.

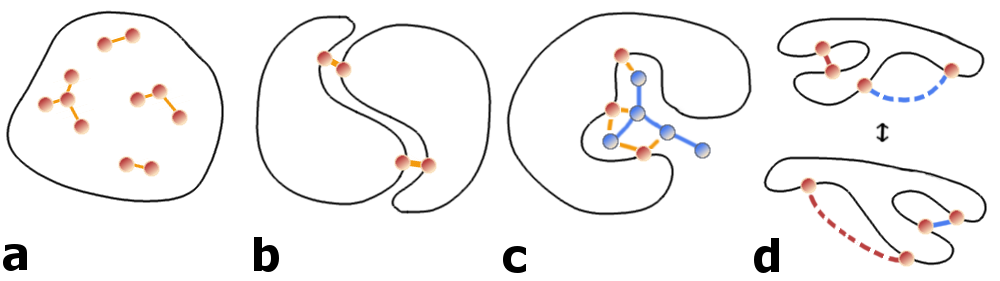
Figure 1.12: Possible sources of coevolutionary signals. a) Physical interactions between intra-domain residues. b) Interactions across the interface of predominantly homo-oligomeric complexes. c) Interactions mediated by ligands or metal atoms. d) Transient interactions due to conformational flexibility.

Many proteins form homo-oligomers with evolutionary conserved interaction surfaces (Figure 1.12 b). Currently it is hard to reliably distinguish intra- and inter-molecular contacts [149]. Anishchenko et al. found that approximately one third of strong co-evolutionary signals between residue pairs at long distances (minimal heavy atom distance >15\(\angstrom\)) can be attributed to interactions across homo-oligomeric interfaces [177]. Several studies specifically analysed co-evolution across homo-oligomeric interfaces for proteins of known structure by filtering for residue pairs with strong couplings at long distances [119,125,149,152,153,186] or used co-evolutionary signals to predict homo-dimeric complexes [150].

It has been proposed that co-evolutionary signals can also arise from ligand or atom mediated interactions between residues or from critical interactions in intermediate folding states (Figure 1.12 c) [179,187]. Confirming this hypothesis, a study showed that the cumulative strength of couplings for a particular residue can be used to predict functional sites [119,178].

Another important aspect is conformational flexibility (Figure 1.12 c). PDB structures used to evaluate coevolution methods represent only rigid snapshots taken in an unnatural crystalline environment. Yet proteins possess huge conformational plasticity and can adopt distinct alternative conformations or adapt shape when interacting with other proteins in an induced fit manner [188]. Several studies demonstrated successfully that coevolutionary signals can capture interactions specific to different distinct conformations [95,119,151,153].

References

95. Morcos, F., Pagnani, A., Lunt, B., Bertolino, A., Marks, D.S., Sander, C., Zecchina, R., Onuchic, J.N., Hwa, T., and Weigt, M. (2011). Direct-coupling analysis of residue coevolution captures native contacts across many protein families. Proc. Natl. Acad. Sci. U. S. A. 108, E1293–301., doi: 10.1073/pnas.1111471108.

96. Cocco, S., Feinauer, C., Figliuzzi, M., Monasson, R., and Weigt, M. (2017). Inverse Statistical Physics of Protein Sequences: A Key Issues Review. arXiv.

178. Marks, D.S., Hopf, T.A., and Sander, C. (2012). Protein structure prediction from sequence variation. Nat. Biotechnol. 30, 1072–1080., doi: 10.1038/nbt.2419.

58. Gouveia-Oliveira, R., and Pedersen, A.G. (2007). Finding coevolving amino acid residues using row and column weighting of mutual information and multi-dimensional amino acid representation. Algorithms Mol. Biol. 2, 12., doi: 10.1186/1748-7188-2-12.

62. Lapedes, A., Giraud, B., Liu, L., and Stormo, G. (1999). Correlated mutations in models of protein sequences: phylogenetic and structural effects. 33, 236–256.

63. Burger, L., and Nimwegen, E. van (2010). Disentangling direct from indirect co-evolution of residues in protein alignments. PLoS Comput. Biol. 6, e1000633., doi: 10.1371/journal.pcbi.1000633.

99. Stein, R.R., Marks, D.S., and Sander, C. (2015). Inferring Pairwise Interactions from Biological Data Using Maximum-Entropy Probability Models. PLOS Comput. Biol. 11, e1004182.

65. Jones, D.T., Buchan, D.W.A., Cozzetto, D., and Pontil, M. (2012). PSICOV: precise structural contact prediction using sparse inverse covariance estimation on large multiple sequence alignments. Bioinformatics 28, 184–90., doi: 10.1093/bioinformatics/btr638.

179. Buslje, C.M., Santos, J., Delfino, J.M., and Nielsen, M. (2009). Correction for phylogeny, small number of observations and data redundancy improves the identification of coevolving amino acid pairs using mutual information. Bioinformatics 25, 1125–31., doi: 10.1093/bioinformatics/btp135.

56. Fodor, A.A., and Aldrich, R.W. (2004). Influence of conservation on calculations of amino acid covariance in multiple sequence alignments. Proteins 56, 211–21.

59. Dunn, S.D., Wahl, L.M., and Gloor, G.B. (2008). Mutual information without the influence of phylogeny or entropy dramatically improves residue contact prediction. Bioinformatics 24, 333–40., doi: 10.1093/bioinformatics/btm604.

102. Kamisetty, H., Ovchinnikov, S., and Baker, D. (2013). Assessing the utility of coevolution-based residue-residue contact predictions in a sequence- and structure-rich era. Proc. Natl. Acad. Sci. U. S. A. 110, 15674–9., doi: 10.1073/pnas.1314045110.

177. Anishchenko, I., Ovchinnikov, S., Kamisetty, H., and Baker, D. (2017). Origins of coevolution between residues distant in protein 3D structures. Proc. Natl. Acad. Sci., 201702664., doi: 10.1073/pnas.1702664114.

180. The UniProt Consortium (2013). Update on activities at the Universal Protein Resource (UniProt) in 2013. Nucleic Acids Res. 41, D43–7., doi: 10.1093/nar/gks1068.

181. Finn, R.D., Coggill, P., Eberhardt, R.Y., Eddy, S.R., Mistry, J., Mitchell, A.L., Potter, S.C., Punta, M., Qureshi, M., and Sangrador-Vegas, A. et al. (2016). The Pfam protein families database: towards a more sustainable future. Nucleic Acids Res. 44, D279–D285., doi: 10.1093/nar/gkv1344.

182. Remmert, M., Biegert, A., Hauser, A., and Söding, J. (2012). HHblits: lightning-fast iterative protein sequence searching by HMM-HMM alignment. Nat. Methods 9, 173–5., doi: 10.1038/nmeth.1818.

183. Espada, R., Parra, R.G., Mora, T., Walczak, A.M., and Ferreiro, D. (2015). Capturing coevolutionary signals in repeat proteins. BMC Bioinformatics 16, 207., doi: 10.1186/s12859-015-0648-3.

184. Toth-Petroczy, A., Palmedo, P., Ingraham, J., Hopf, T.A., Berger, B., Sander, C., Marks, D.S., Alexander, P., He, Y., and Chen, Y. et al. (2016). Structured States of Disordered Proteins from Genomic Sequences. Cell 167, 158–170.e12., doi: 10.1016/j.cell.2016.09.010.

174. Ashkenazy, H., Unger, R., and Kliger, Y. (2009). Optimal data collection for correlated mutation analysis. Proteins 74, 545–55., doi: 10.1002/prot.22168.

185. Avila-Herrera, A., and Pollard, K.S. (2015). Coevolutionary analyses require phylogenetically deep alignments and better null models to accurately detect inter-protein contacts within and between species. BMC Bioinformatics 16, 268.

149. Uguzzoni, G., John Lovis, S., Oteri, F., Schug, A., Szurmant, H., and Weigt, M. (2017). Large-scale identification of coevolution signals across homo-oligomeric protein interfaces by direct coupling analysis. Proc. Natl. Acad. Sci. 114, E2662—–E2671., doi: 10.1073/pnas.1615068114.

169. Franceus, J., Verhaeghe, T., and Desmet, T. (2016). Correlated positions in protein evolution and engineering. J. Ind. Microbiol. Biotechnol., 1–9., doi: 10.1007/s10295-016-1811-1.

119. Hopf, T.A., Colwell, L.J., Sheridan, R., Rost, B., Sander, C., and Marks, D.S. (2012). Three-dimensional structures of membrane proteins from genomic sequencing. Cell 149, 1607–21., doi: 10.1016/j.cell.2012.04.012.

110. Feinauer, C., Skwark, M.J., Pagnani, A., and Aurell, E. (2014). Improving contact prediction along three dimensions. 19.

125. Wang, Y., and Barth, P. (2015). Evolutionary-guided de novo structure prediction of self-associated transmembrane helical proteins with near-atomic accuracy. Nat. Commun. 6, 7196.

152. Sutto, L., Marsili, S., Valencia, A., and Gervasio, F.L. (2015). From residue coevolution to protein conformational ensembles and functional dynamics. Proc. Natl. Acad. Sci. U. S. A., 1508584112., doi: 10.1073/pnas.1508584112.

153. Jana, B., Morcos, F., and Onuchic, J.N. (2014). From structure to function: the convergence of structure based models and co-evolutionary information. Phys. Chem. Chem. Phys. 16, 6496., doi: 10.1039/c3cp55275f.

186. Lee, B.-C., and Kim, D. (2009). A new method for revealing correlated mutations under the structural and functional constraints in proteins. Bioinformatics 25, 2506–13., doi: 10.1093/bioinformatics/btp455.

150. Dos Santos, R.N., Morcos, F., Jana, B., Andricopulo, A.D., and Onuchic, J.N. (2015). Dimeric interactions and complex formation using direct coevolutionary couplings. Sci. Rep. 5, 13652.

187. Ovchinnikov, S., Kim, D.E., Wang, R.Y.-R., Liu, Y., DiMaio, F., and Baker, D. (2015). Improved de novo structure prediction in CASP11 by incorporating Co-evolution information into rosetta. Proteins., doi: 10.1002/prot.24974.

188. Noel, J.K., Morcos, F., and Onuchic, J.N. (2016). Sequence co-evolutionary information is a natural partner to minimally-frustrated models of biomolecular dynamics. F1000Research 5., doi: 10.12688/f1000research.7186.1.

151. Sfriso, P., Duran-Frigola, M., Mosca, R., Emperador, A., Aloy, P., and Orozco, M. (2016). Residues Coevolution Guides the Systematic Identification of Alternative Functional Conformations in Proteins. Structure 24, 116–126., doi: 10.1016/j.str.2015.10.025.